はじめに
物体検出してますか。
物体検出モデルは予測した物体を囲むボックス(バウンディングボックス)、識別した物体のクラス、各予測に対する信頼度を出力します。一般的なモデルの評価には適合率や再現率といった評価指標が存在しますが、そのままではバウンディングボックスボックスや信頼度を評価できません。
物体検出モデルの良さの指標は、以下のようなふるまいをすることが期待されます。
- クラス:正解クラスと一致したとき高くなる
- ボックス:正解のボックスと距離が近ければ近いほど高くなる
- 信頼度:信頼度の値が大きいにも関わらずクラス・ボックスが誤っていたときは低くなる
物体検出においては、上記のようにふるまうAP (Average Precision) や mAP (mean Average Precision) といった尺度が使われます。これを計算するために、まずはボックスを評価できる指標を作りましょう。
IoU
ボックスの重なりを評価するための指標はIoU (Intersection over Union) 、もしくはJaccard 係数と呼ばれます。
IoU = \frac{2つのボックスの積集合の面積}{2つのボックスの和集合の面積}
IoUは正解のボックスと予測のボックスが重なれば重なるほどよくなる指標で、1から0の値を取り、完全に重なると1、全く重ならないと0になります。

AP
IoUについて閾値を定めれば、予測した各ボックスについてTrueとFalseを判定でき、通常のニューラルネットワークと同様に各クラスについて適合率や再現率を計算することができます。しかし、これだけでは信頼度を考慮できません。
信頼度を考慮するためには、各クラスについて信頼度が高い順に「採点」をしていって、早い段階で全ての正解ボックスが予測され尽くせば指標が高くなるべきです。これはランキングの評価と捉えることができます。一般にランクをもつデータを評価する指標として、AP (Average Precision) という指標が存在します。
APの計算方法は以下のとおりです。ランキング順にサンプルを増やしていって、複数の適合率と再現率を得ます。それぞれを縦軸・横軸としてプロットし、描かれたカーブ(PR曲線と呼ばれる)の下側の面積がAPです。
物体検出のデータを例に説明すると、まず信頼度順に予測されたボックスを並べ、順番に現時点での適合率と再現率を計算します。
この時、
となり、不正解の時がくっと下がり正解すると少し上がるような関数になります。
再現率 = \frac{ここまで正解したボックス数(正解すれば1増える)}{最終的に出してほしい正解ボックス数(ずっと固定)}となり、正解すると正解ボックスの逆数分大きくなり、不正解のときは増えも減りもしない関数になります。
例えば、以下は正解ボックスが5個ある教師データに対して予測データが10個あるデータの例です。
"StopSign"と予測されたPredicted BBoxの検出結果
| Sorted Number | Confidence Score(%) | Correct? | Precision | Recall |
|---|---|---|---|---|
| #1 | 96 | True | 1/1 = 1 | 1/5 = 0.2 |
| #2 | 92 | True | 2/2 = 1 | 2/5 = 0.4 |
| #3 | 89 | False | 2/3 = 0.667 | 2/5 = 0.4 |
| #4 | 88 | False | 2/4 = 0.5 | 2/5 = 0.4 |
| #5 | 84 | False | 2/5 = 0.4 | 2/5 = 0.4 |
| #6 | 83 | True | 3/6 = 0.5 | 3/5 = 0.6 |
| #7 | 80 | True | 4/7 = 0.571 | 4/5 = 0.8 |
| #8 | 78 | False | 4/8 = 0.5 | 4/5 = 0.8 |
| #9 | 74 | False | 4/9 = 0.444 | 4/5 = 0.8 |
| #10 | 72 | True | 5/10 = 0.5 | 5/5 = 1.0 |
引用:【物体検出】mAP ( mean Average Precision ) の算出方法
この表についてx軸を再現率 (Recall)、y軸を適合率 (Precision) を取ってグラフ(PR曲線)を書きます。
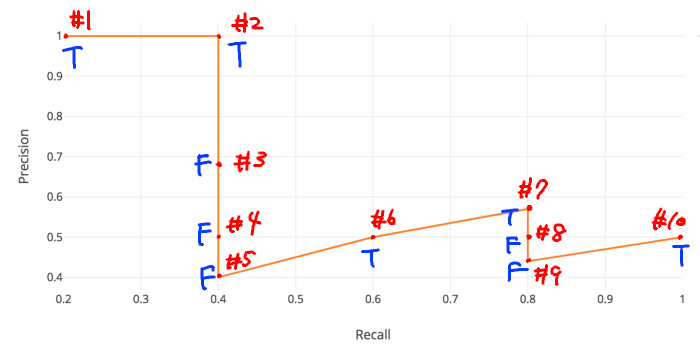
引用(一部改変):mAP (mean Average Precision) for Object Detection
この時、Trueになっている点の適合率の平均値がAP、つまり平均適合率です。
AP = \frac{(1+1+0.5+0.571+0.5)}{5} = 0.7142
この値はデータが大きくなるにつれてオレンジ色の線の下の面積に近付きます。
すなわち、rを再現率、pを適合率とすると
AP = \int_0^1 p(r) dr
信頼度が高い順に並べて、正解し続ければこのオレンジの線は上に留まりながら右に進み続けることになり、この時APの値が最大であり1となります。逆に信頼度が高いにも関わらず不正解し続けるとオレンジの線は急激に下がり、最終的なAPの値も0に近づきます。
APを計算するための関数はsklearnモジュール内に存在します。例えば上の表を計算するときは以下のようになります。リスト内は信頼度順に並んでいなくても構いません。
from sklearn.metrics import average_precision_score
y_true = [True, True, False, False, False, True, True, False, False, True]
y_score = [96, 92, 89, 88, 84, 83, 80, 78, 74, 72]
average_precision = average_precision_score(y_true, y_score)
print(average_precision)
APの値はボックスについて定めた閾値によって変化するので、閾値xを定めた時のAPはAPxと表記されることがあります。(例:AP50、AP75)
mAP
APは各クラスに対して計算できます。モデル全てのクラスに対してAPを算出し、平均を取った値がmAP (mean Average Precision) です。
実際のAPやmAPの計算は上記を元に近似や若干異なる計算方法が使われることもあります。よしなに。
参考文献
【物体検出】mAP ( mean Average Precision ) の算出方法
mAP (mean Average Precision) for Object Detection
レコメンドつれづれ ~第3回 レコメンド精度の評価方法を学ぶ~
Header photo on PIXNIO(一部改変)