NumPyとPyTorchでゼロから学ぶニューラルネットワーク

2020.07.20

NumPyとPyTorchでゼロから学ぶニューラルネットワーク

numpy python pytorch ニューラルネットワーク深層学習誤差逆伝播法

対象読者

初学者向けの内容となっていますので、ほぼゼロ(行列の積)から復習します。
ゼロから学ぶディープラーニングの内容をまとめて、pytorchでも実装する内容になっています。

行列の積

ニューラルネットワークでは、行列の積が重要であるため、基本的な行列の積について復習します。

行列の積は以下のように計算できます。

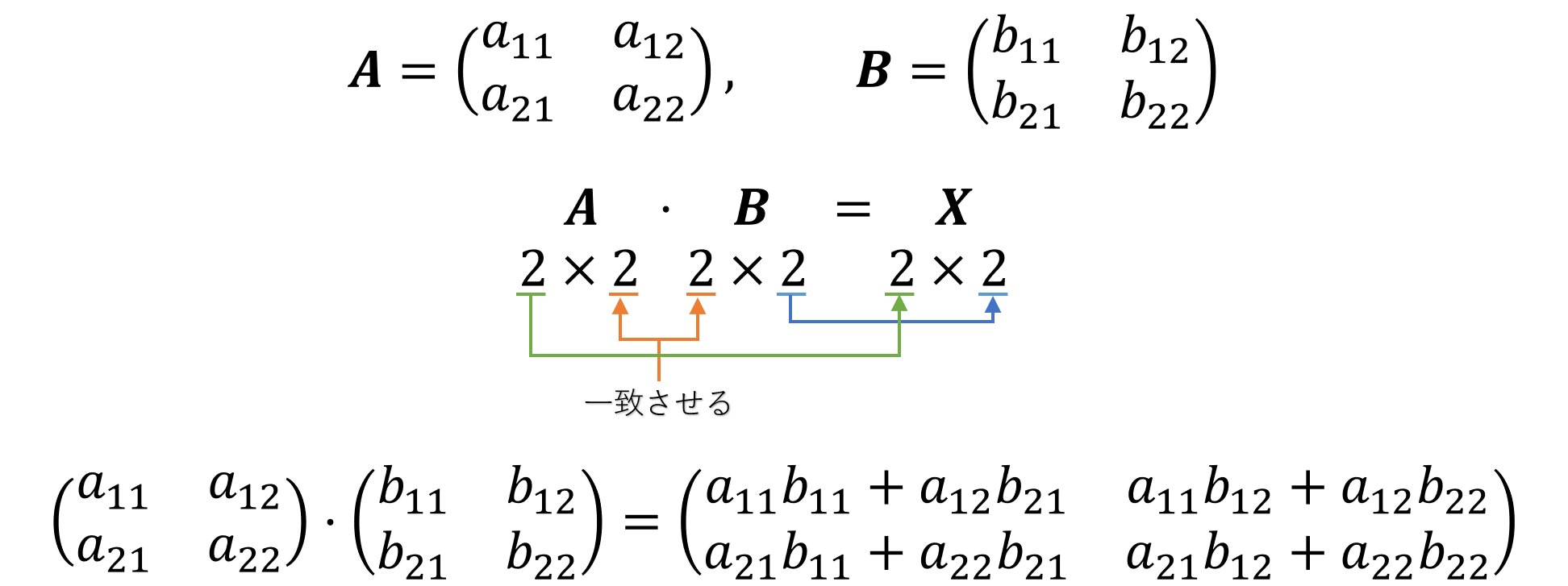
以下の例では、２つの行列の次元が異なっています。
注意ポイントは、スカラーとは異なり、行列の内側の次元を一致させなければならないというルールがあります。これは、計算方法を見てもらうとわかると思います。
また、このようにして、得られる行列は、２つの行列の外側の次元になっていることがわかります。

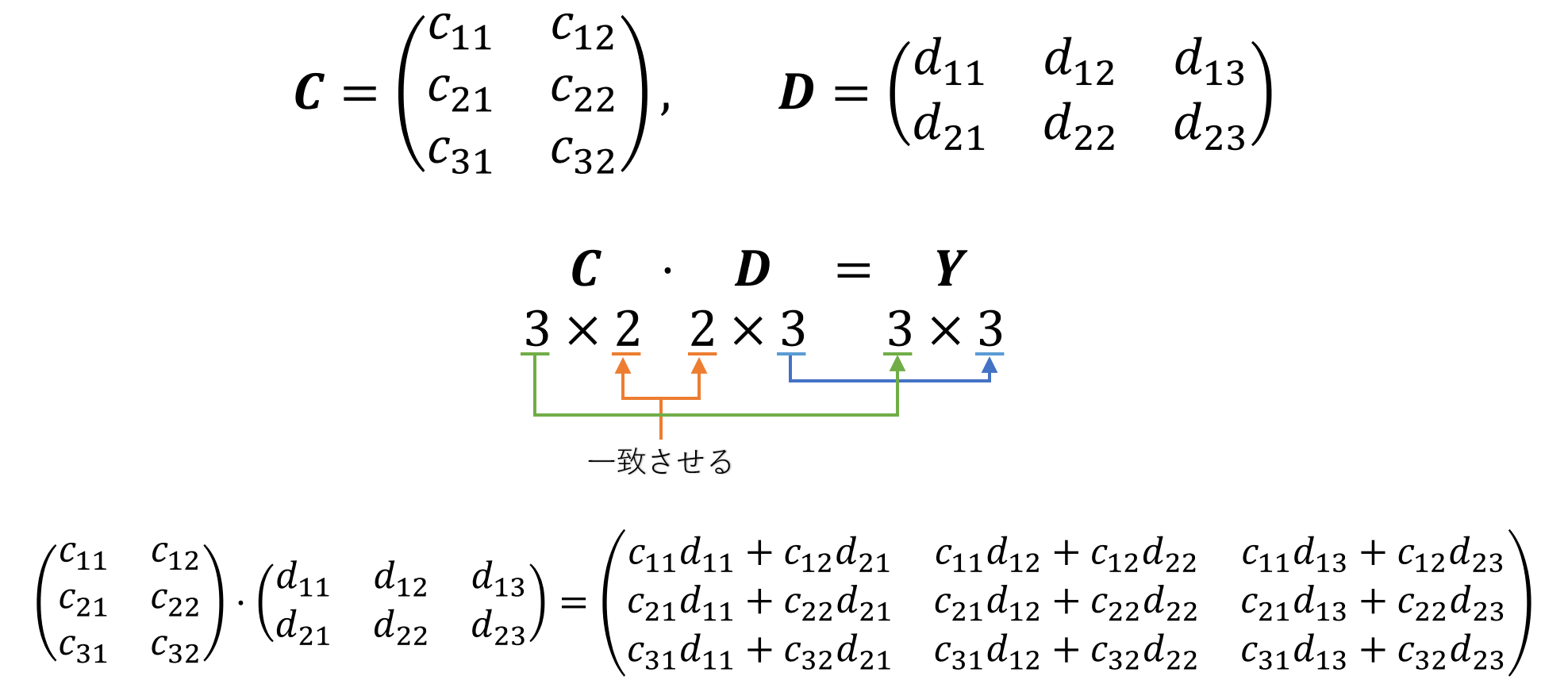
$C \in \mathbb{R}^{3\times2}$ と $D \in \mathbb{R}^{2\times3}$ の各要素を適当に設定して、numpyで $C \cdot D$ と $D \cdot C$ を計算してみます。

import torch
import torch.nn as nn
import torch.optim as optimizers
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

C = np.arange(3*2).reshape(3, 2)
D = np.arange(2*3).reshape(2, 3)
print("C = \n{}".format(C))
print("D = \n{}".format(D))
print("C・D = \n {}".format(np.dot(C, D)))
print("C・D = \n {}".format(C @ D))

C =
[[0 1]
 [2 3]
 [4 5]]
D =
[[0 1 2]
 [3 4 5]]
C・D =
 [[ 3  4  5]
 [ 9 14 19]
 [15 24 33]]
C・D =
 [[ 3  4  5]
 [ 9 14 19]
 [15 24 33]]

print("D・C = \n {}".format(np.dot(D, C)))
print("D・C = \n {}".format(D @ C))

D・C =
 [[10 13]
 [28 40]]
D・C =
 [[10 13]
 [28 40]]

この例では、 $C \cdot D$ と $D \cdot C$ の両方で計算できます。これは、積の順番を入れ替えても２つの行列の内側の次元が一致するためです。
しかし、積の順番を入れ替えても、結果が一致するとは限りません。ここでは、行列の次元数が異なっていることがわかります。

また、行列の積では順序を変えると、結果が変わってしまう場合やそもそも計算できない場合が存在します。

ニューラルネットワーク

ここでは、ニューラルネットワークの説明のために、三層ニューラルネットワーク（二値分類問題）を用いて説明します。
※以下では、簡単のために、バイアスは0として考えています。

問題設定

$x_1$ と $x_2$ が与えられたときに、クラス1かクラス2のどちらのlabelがついているか予測する問題を考えます。

データの確認

train_data = pd.read_csv("./sample_data/sample.csv")
train_data

	x1	x2	class1	class2
0	0	0	0	1
1	0	1	1	0
2	1	1	0	1
3	1	0	1	0

※XORの真理値表

可視化してみると、以下のように図のようになります。

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
for c in set(train_data.class1):
    df_classes = train_data[train_data['class1'] == c]
    ax.scatter(data=df_classes, x='x1', y='x2', label='class{}'.format(c+1))
ax.legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.show()

ネットワーク構造

層が３つあるため、三層ニューラルネットワークと呼ばれます。
上記のようなデータを考えると、三層ニューラルネットワークは以下のように設計できます。

入力：特徴量
出力：データが各クラスに属する確率

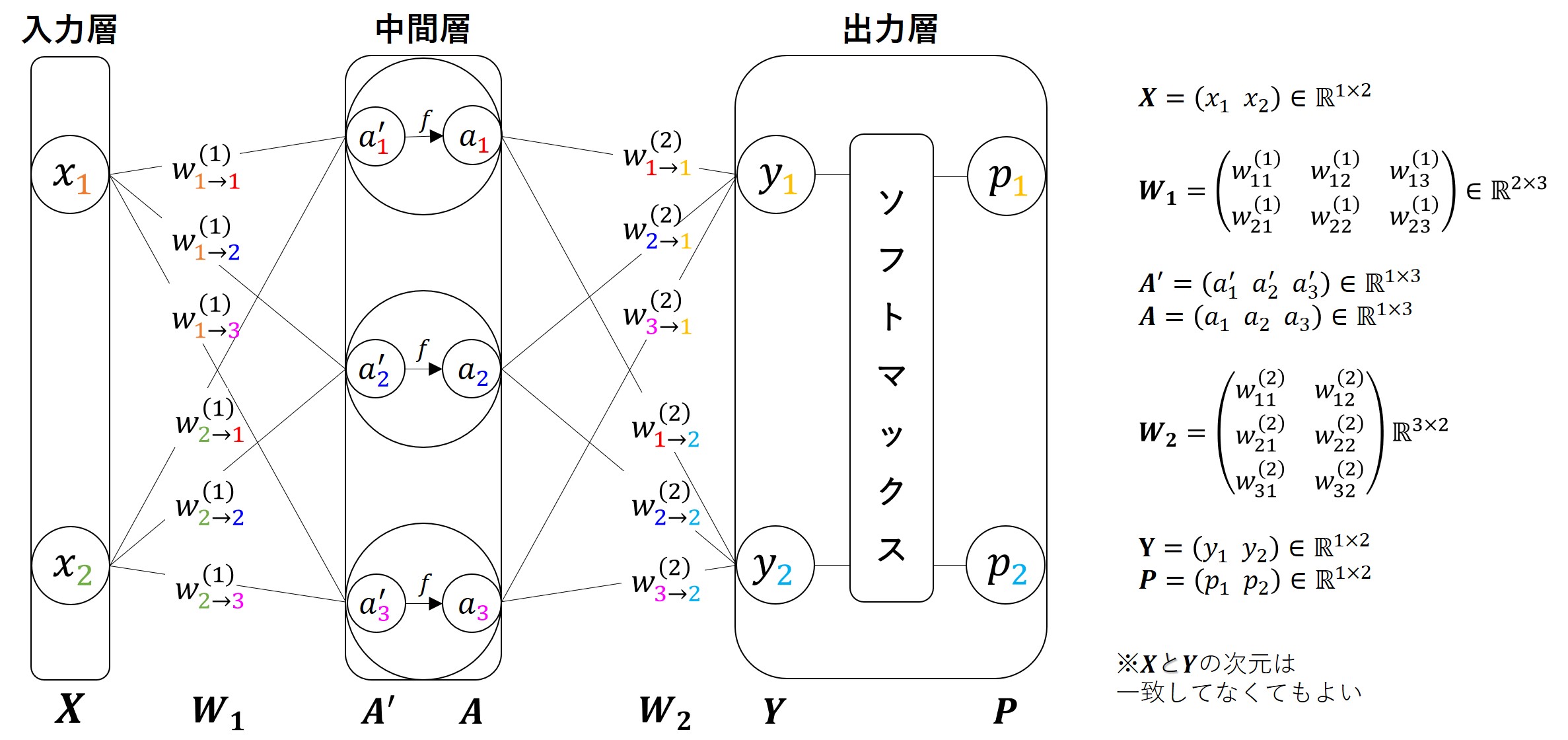
丸( $x_1, x_2, a_1^{\prime}, a_2^{\prime} ,a_3^{\prime} ,a_1, a_2, a_3, y_1, y_2, p_1, p_2$ )で表現されているニューロンを繋ぐ線の一つ一つに重みが設定されています。
これらの重みが的確に設定されていると、正しく分類ができるようなネットワークということになります。
行列を使わずに表現することもできますが、式を簡潔に書くために重みを行列で表しています。

数式

次に、上記で説明したネットワークを数式で表現してみます。冒頭で説明された行列の積で表現することができます。

ネットワークの設計

決められた入出力に対して、①中間層の層数、②中間層のニューロン数などのパラメータはある程度自由にカスタマイズできます。

e.g.)上記のネットワーク構造を中間層のニューロン数を4つにすることを考えます。

$W_{1} \in \mathbb{R}^{2 \times 4}$ に変更したい
行列の積の性質上、 $A^{\prime} \in \mathbb{R}^{1 \times 4}$ に変更する必要があります
$A \in \mathbb{R}^{1 \times 4}$ になります
行列の積の性質上、 $W_{2} \in \mathbb{R}^{4 \times 2}$ に変更する必要があります

行列の次元数を一致させなければいけない点に気を付ければ、パラメータの個数は自由にカスタマイズできます。

活性化関数

上記の数式で、 $f$ が登場しています。これを活性化関数とよび、重みをかけた後に値を変換するために使われる関数です。深層学習では、活性化関数に非線形な関数を適用することでニューラルネットワークの表現力を豊かにしています。

以下では、代表的な非線形な活性化関数を紹介します。

シグモイド関数
$Sigmoid(x) = \displaystyle \frac{1}{1+e^{-x}}$
ReLU関数
$ReLU(x) = \begin{cases} x & x \geqq 0 \\ 0 & x < 0 \ \end{cases}$

$f$ に行列を入力するにはどうすれば良いのかと疑問に思った方もいるかもしれませんが、ここでは、 $f$ に、 $A^\prime$ のそれぞれの要素を入力するとします。そのようにして出力された値を同じ順番に並べて、 $A$ として変換しています。

ソフトマックス関数

出力を確率の定義を満たす([0,1]の値で総和が1)値に変換します

{\rm Softmax}((y_1, y_2)) = (p_1, p_2)

p_1 = \displaystyle \frac{\exp{(y_1)}}{\exp{(y_1)}+\exp{(y_2)}}

p_2 = \displaystyle \frac{\exp{(y_2)}}{\exp{(y_1)}+\exp{(y_2)}}

※出力が2つである場合は、シグモイド関数と等しい

※出力が $n$ 個である場合のソフトマックス関数
$p_i = \frac{\exp{(y_i)}}{\sum_{i}^{n} {\exp{(y_i)}}}$

ソフトマックス関数の例

$y_1=30, y_2=60$ がソフトマックス関数に入力されたとき、各ラベルの予測確率はいくつになるか考えます。

y1 = 30
y2 = 60
p1 = np.exp(y1) / (np.exp(y1) + np.exp(y2))
p2 = np.exp(y2) / (np.exp(y1) + np.exp(y2))
print("p1 = {}".format(p1))
print("p2 = {}".format(p2))
print("p1 + p2 = {}".format(p1 + p2))

p1 = 9.3576229688393e-14
p2 = 0.9999999999999064
p1 + p2 = 1.0

p1とp2が[0,1] の値で和が1であるため、y1とy2が確率の定義を満たすように変換されたことがわかります。

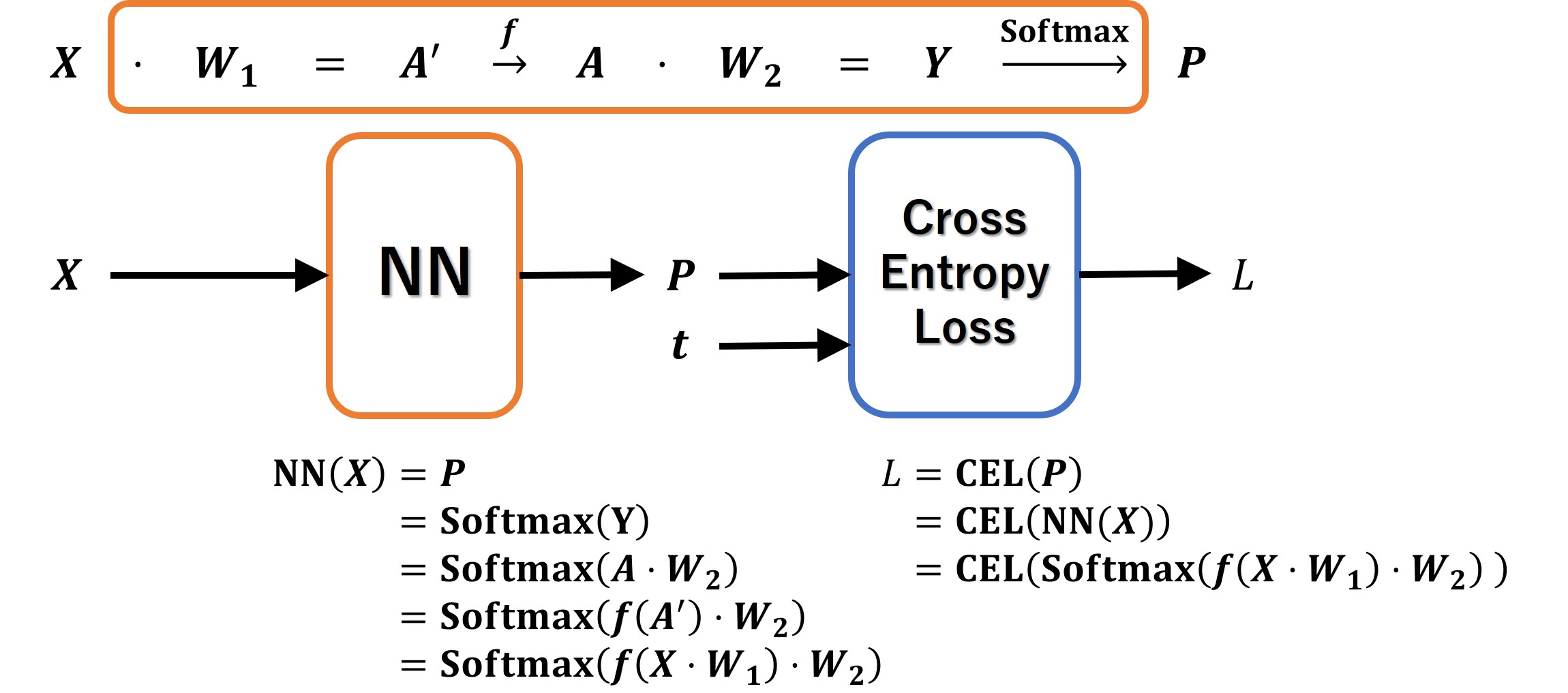
順伝播

ニューラルネットワーク(教師あり学習)の順伝播

前の層からの入力に対して、右から重み $W$ を掛けます
1の結果を適当な関数 $f$ で変換して、次の層の入力とします
上記の操作を繰り返します
出力層まで来たら、出力値を誤差関数に代入して、誤差を出力します

クロスエントロピー誤差関数

分類問題での誤差関数として、クロスエントロピー誤差関数がよく使われます。

L = {\rm CrossEntropyLoss}(p_1, p_2, t_1, t_2) = -\sum_{i=1}^{2} t_{i}\log{p_{i}}

$t_{i}$ ：正解ラベルのときだけ1

e.g.)ラベル1の予測確率が70%で、ラベル2の予測確率が30%と出力されたとき、ラベル1が正解だった場合

L = - (1 \cdot \log{0.7} + 0 \cdot \log{0.3})

※出力が $l$ クラスである場合のクロスエントロピー誤差関数
$L = {\rm CrossEntropyLoss}(p_1, p_2,...,p_n, t_1, t_2, ..., t_n) = -\sum_{i=1}^{l} t_{i}\log{p_{i}}$

式(4)では一つのデータ分の誤差しか求めていないため、実際に誤差を計算するときは、すべてのデータ分の誤差を平均する必要があります。

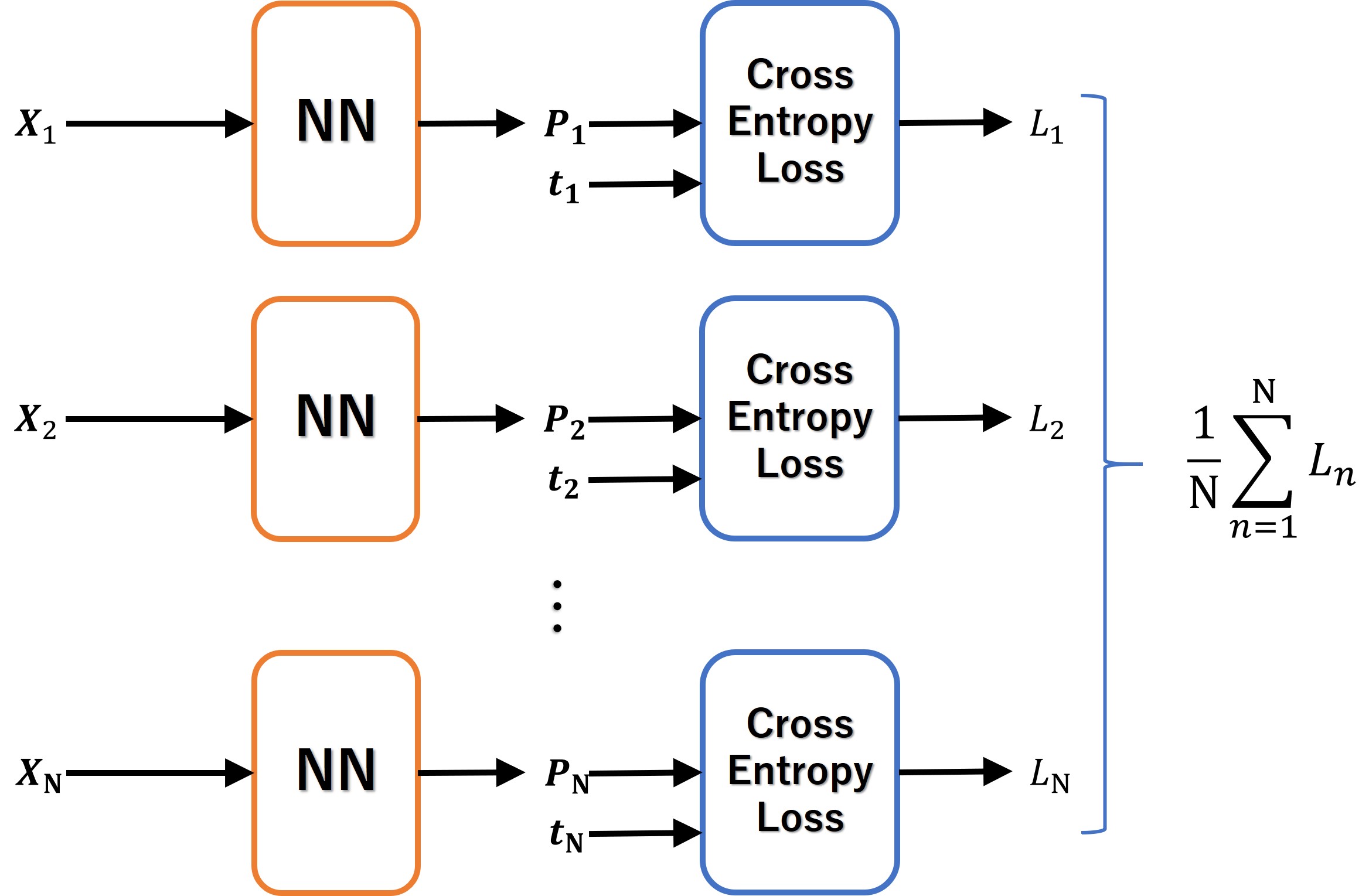
ここで実際に、上記をコードで実装してみます。

三層ニューラルネットワークの $W_1$ と $W_2$ を適当に定めて、train_dataをどれくらいの誤差で予測できるかnumpyで計算してみます
※活性化関数 $f$ はシグモイド関数を使用しています。

train_data_np = train_data.values
# 入力データ
X1 = train_data_np[0][:2]
X2 = train_data_np[1][:2]
X3 = train_data_np[2][:2]
X4 = train_data_np[3][:2]
# 正解データ
T1 = train_data_np[0][2:4]
T2 = train_data_np[1][2:4]
T3 = train_data_np[2][2:4]
T4 = train_data_np[3][2:4]

def sigmoid(X):
    return 1 / (1 + np.exp(-X))

def softmax(Y):
    c = np.max(Y)
    exp_Y = np.exp(Y - c)  # オーバーフロー対策
    sum_exp_Y = np.sum(exp_Y)
    P = exp_Y / sum_exp_Y
    return P

def cross_entropy_error(P, T):
    delta = 1e-7
    return -np.sum(T * np.log(P + delta))

W1 = np.array([[1.0, 0.1, 0.9],
               [1.2, 1.1, 0.7]])
W2 = np.array([[1.0, 0.8],
               [0.0, 0.5],
               [1.1, 0.9]])

L = 0
# X1
A_prime = X1 @ W1
A = sigmoid(A_prime)
Y = A @ W2
P = softmax(Y)
L1 = cross_entropy_error(P, T1)
L += L1
# X2
A_prime = X2 @ W1
A = sigmoid(A_prime)
Y = A @ W2
P = softmax(Y)
L2 = cross_entropy_error(P, T2)
L += L2
# X3
A_prime = X3 @ W1
A = sigmoid(A_prime)
Y = A @ W2
P = softmax(Y)
L3 = cross_entropy_error(P, T3)
L += L3
# X4
A_prime = X4 @ W1
A = sigmoid(A_prime)
Y = A @ W2
P = softmax(Y)
L4 = cross_entropy_error(P, T4)
L += L4
print("Loss:{}".format(L))

Loss:2.7611593717597174

データを一括処理すると、以下のようにかけます。

def softmax_batch(Y):
    return np.exp(Y) / np.sum(np.exp(Y), axis = 1, keepdims = True)

X = np.concatenate([X1, X2, X3, X4]).reshape(4, 2)
T = np.concatenate([T1, T2, T3, T4]).reshape(4, 2)
A_prime = X @ W1
A = sigmoid(A_prime)
Y = A @ W2
P = softmax_batch(Y)
L = cross_entropy_error(P, T)
print("Loss:{}".format(L))

Loss:2.7611593717597174

$W_1$ と $W_2$ を修正することで、誤差を小さくしてみます。

W1 = np.array([[2.8, 0.1, 0.1],
               [2.3, 0.21, 0.1]])
W2 = np.array([[2.0, 0.8],
               [0.1, 0.5],
               [0.3, 1.9]])

X = np.concatenate([X1, X2, X3, X4]).reshape(4, 2)
T = np.concatenate([T1, T2, T3, T4]).reshape(4, 2)
A_prime = X @ W1
A = sigmoid(A_prime)
Y = A @ W2
P = softmax_batch(Y)
L = cross_entropy_error(P, T)
print("Loss:{}".format(L))

Loss:2.5798492272716675

このように重み(W1, W2)を変更すると、誤差を小さくすることができます。
今回は適当に重みを変更しましたが、最適化手法(SGDやAdam等)を使うことで最適な重みを計算することができます。

クラス1、クラス２に分類する領域を可視化すると以下のようになります。

x1 = np.arange(-5, 5, 0.01)
x2 = np.arange(0, 6, 0.01)
xx, yy = np.meshgrid(x1, x2)
xx = xx.flatten()
yy = yy.flatten()
xy = np.c_[xx, yy]
A_prime = xy @ W1
A = sigmoid(A_prime)
Y = A @ W2
P = softmax_batch(Y)

plt.scatter(xy[np.argmax(P, 1) == 0].T[0], xy[np.argmax(P, 1) == 0].T[1], label='predict_class{}'.format(1), c='lightskyblue')
plt.scatter(xy[np.argmax(P, 1) == 1].T[0], xy[np.argmax(P, 1) == 1].T[1], label='predict_class{}'.format(2), c='orange')
for c in set(train_data.class1):
    df_classes = train_data[train_data['class1'] == c]
    plt.scatter(data=df_classes, x='x1', y='x2', label='class{}'.format(c+1))
plt.legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.show()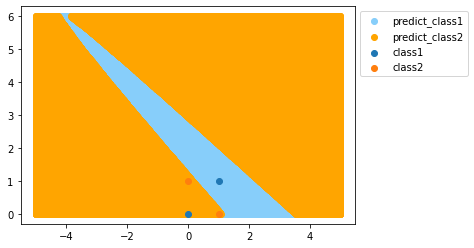

明らかに分離できていないことがわかります。

pytorch

pytorchで上記と同様なコードを実装してみます。ネットワーク構造も同じです。

class NN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(NN, self).__init__()
        self.l1 = nn.Linear(input_dim, hidden_dim, bias=False)
        self.a = nn.Sigmoid()
        self.l2 = nn.Linear(hidden_dim, output_dim, bias=False)
        self.layers = [self.l1, self.a, self.l2]
    def forward(self, x):
        for layer in self.layers:
            x = layer(x)
        return x

torch.manual_seed(0)
input_dim = 2  # 入力層の次元数(画像データを一次元に変換したときの次元数)
hidden_dim = 4  # 中間層の次元数(中間層のニューロン数)
output_dim = 2  # 出力層の次元数(class1 or class2)
# モデルの構築
model = NN(input_dim, hidden_dim, output_dim)

# 誤差関数の定義
compute_loss = nn.CrossEntropyLoss()
# 最適化手法の定義
optimizer = optimizers.Adam(model.parameters(),
                            lr=0.001,
                            betas=(0.9, 0.999),
                            amsgrad=True)

def train_step(x, t):
    model.train()  # モデルを訓練モードに設定する
    preds = model(x)  # modelにxを代入して、予測させる
    loss = compute_loss(preds, t)  # 予測値と正解との誤差を求める
    optimizer.zero_grad()  # 勾配を初期化する
    loss.backward()  # 勾配を計算する
    optimizer.step()  # パラメータを更新する
    return loss, preds

# numpy -> tensor
X_tensor = torch.FloatTensor(X)
T_tensor = torch.tensor(T.T[0], dtype=torch.int64)

torch.manual_seed(0)
# モデルの学習
for epoch in range(10000):
    # 訓練パート
    loss, preds = train_step(X_tensor, T_tensor)
    if epoch % 1000 == 0:
        print('epoch {} : loss {}'.format(epoch, loss.item()))

epoch 0 : loss 0.7091774940490723
epoch 1000 : loss 0.6213149428367615
epoch 2000 : loss 0.29985612630844116
epoch 3000 : loss 0.14419220387935638
epoch 4000 : loss 0.08603499829769135
epoch 5000 : loss 0.059611424803733826
epoch 6000 : loss 0.045122966170310974
epoch 7000 : loss 0.03611883148550987
epoch 8000 : loss 0.030027955770492554
epoch 9000 : loss 0.02565212920308113

学習させた結果、クラス１、クラス２に分類する領域を可視化してみてみます。

x1 = np.arange(-5, 5, 0.01)
x2 = np.arange(0, 6, 0.01)
xx, yy = np.meshgrid(x1, x2)
xx = xx.flatten()
yy = yy.flatten()
xy = np.c_[xx, yy]
xy_tensor = torch.FloatTensor(xy)
p_tensor = model(xy_tensor)

plt.scatter(xy_tensor[torch.argmax(p_tensor, 1) == 0].T[0],
            xy_tensor[torch.argmax(p_tensor, 1) == 0].T[1],
            label='predict_class{}'.format(1), c='lightskyblue')
plt.scatter(xy_tensor[torch.argmax(p_tensor, 1) == 1].T[0],
            xy_tensor[torch.argmax(p_tensor, 1) == 1].T[1],
            label='predict_class{}'.format(2), c='orange')
for c in set(train_data.class1):
    df_classes = train_data[train_data['class1'] == c]
    plt.scatter(data=df_classes, x='x1', y='x2', label='class{}'.format(c+1))
plt.legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.show()

この4つの点に関しては、分類できるような重みを設定することができました。

誤差逆伝播法

実装は前節までで終了です。ここからは、とばした最適化手法の中身について触れていこうと思います。

ニューラルネットワークといえば、誤差逆伝播法と言うキーワードが一緒に登場すると思います。しかし、本記事では登場せずにニューラルネットワークを学習までしてしまいました。
本節では、誤差逆伝播法がなぜ必要なのかと計算する方法をイメージ的に説明したいと思います。

なぜ必要なのか

前節では、実際に最適化手法のAdamを使って、ニューラルネットワークの重みを学習しました。手動で重みを変えながら損失が下がるかどうかを確かめるより、効率的に重みを更新できたかと思います。それでは、どのようにして、重みを更新しているのでしょうか？

あくまでイメージですが、誤差関数が以下のような坂道であると考えたときに、最適化手法により、球が転がるように重みが更新されていきます。谷に落ちるとそこで更新が終了します。視覚的には、進む方向は明らかなのですが、数式的にはどちらに更新するかわかりません。このときに進む方向を決定するために勾配(傾き)が必要であり、この誤差関数の傾きを求めるために誤差逆伝播法が必要なのです。

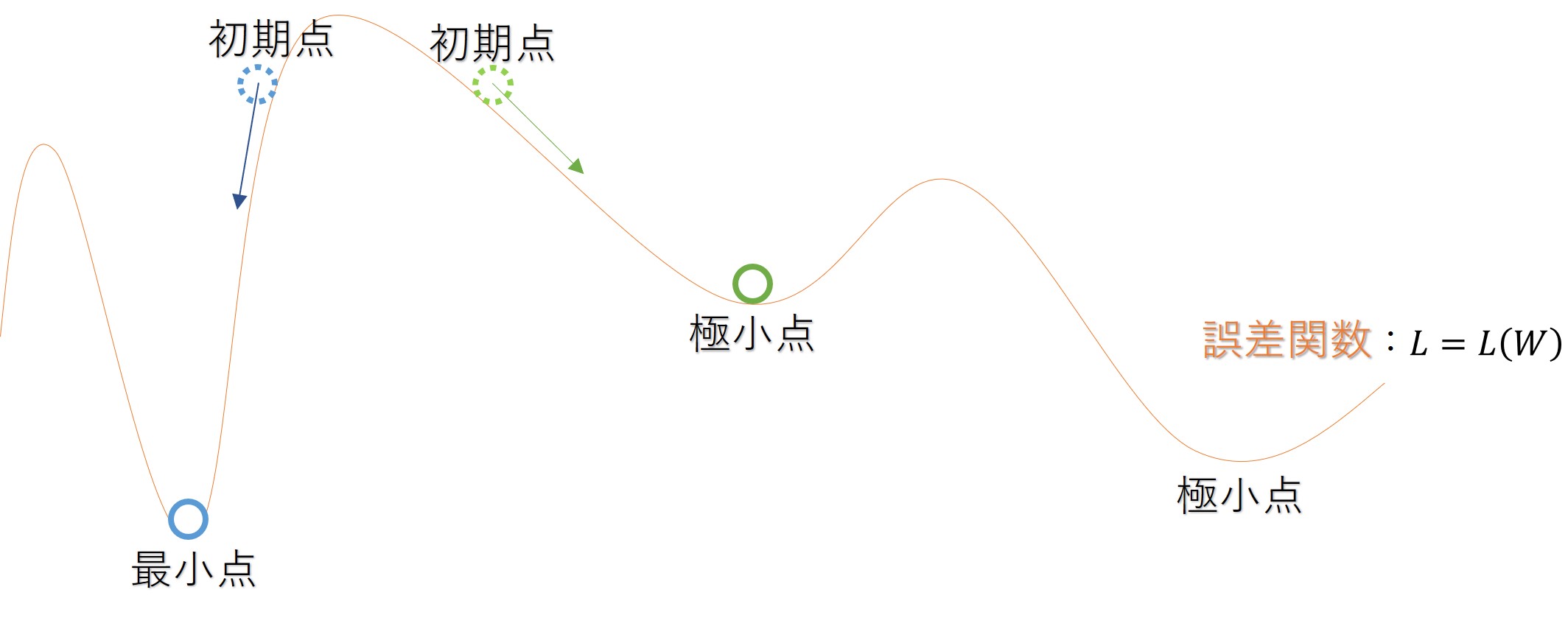
まとめると、誤差逆伝播は、単に誤差関数を微分しているだけなのです。

最適化手法についての踏み込んだ話は本ブログでは割愛しますが、実際に、シグモイド関数を例に誤差逆伝播法を考えてみます。

計算グラフ

まずはじめに、誤差逆伝播法で説明を簡単にするために計算グラフについて説明します(実際、計算グラフを使用しなくても誤差逆伝播法は計算できます)。
右から左へ計算が行われていることがわかります。このことを順伝播といいます。

リンゴの例

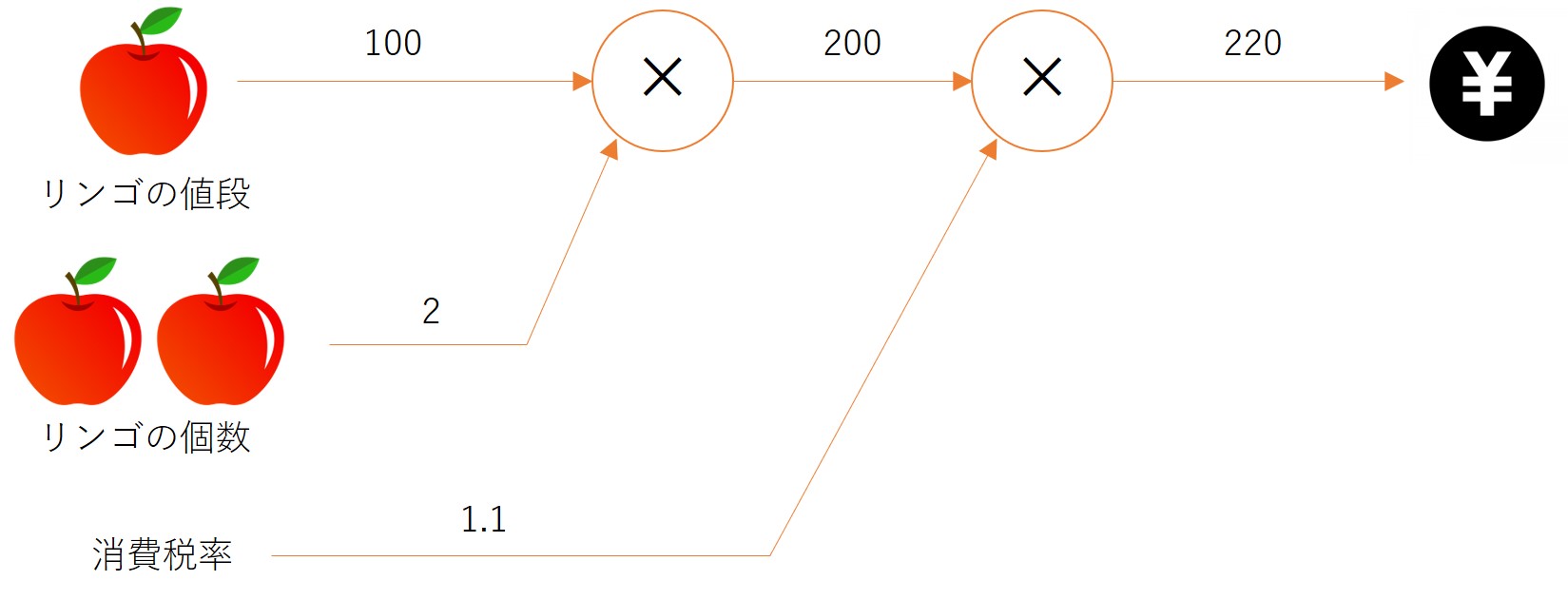
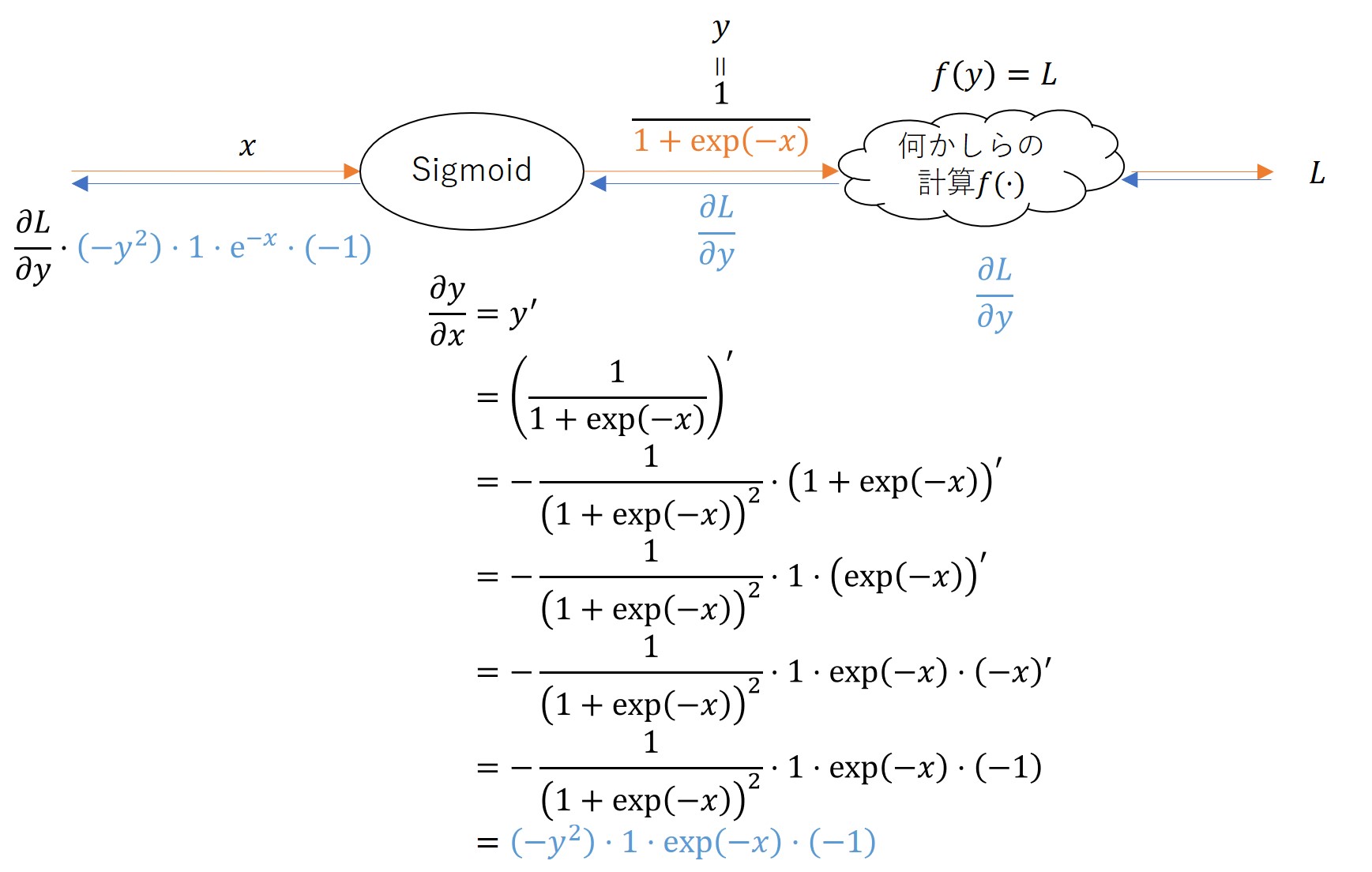
シグモイド関数の例

オレンジの矢印は順伝播であり、青の矢印が逆伝播を意味しています。

誤差逆伝播は逆順に微分していて、つまりは、合成関数の微分をしているだけであることがわかります。

以下のように、手計算で微分を導出する手順に似ていて、結果も一致します。

このような計算はそれぞれは単純ではありますが、このような微分をニューラルネットワーク全体で考えるのは面倒なだけでなく、ミスをする可能性が高くなります。
よって、Pytorchのような深層学習フレームワークを用いるメリットは、順伝播を定義することで、自動でこのような微分を計算できる点にあります。

参考文献

深層学習(機械学習プロフェッショナルシリーズ)

ゼロから作るDeep Learning――Pythonで学ぶディープラーニングの理論と実装

詳解ディープラーニング第2版 TensorFlow/Keras・PyTorchによる時系列データ処理

\ いいなと思ったらシェア /

ブログトップに戻る