はじめに
データ分析において対象となるデータを可視化することは重要だとしばしば言われます。数値の羅列を見ているだけではデータ間の関係性を視覚的に発見できることがあるからです。
データ可視化の練習として、以前Tommyさんのblog記事をご紹介しました。今回は、Excelでできるデータドリブン・マーケティングという本の第3章をPythonで実装してみます。
データの読み込み
この本には演習用のデータとして、エクセルのファイルが付いています。そのファイルをcsv形式にしてダウンロードし、保存します。ファイル名はalcohol.csvとしました。
import pandas as pd
df = pd.read_csv('alcohol.csv')Google Colaboratoryを利用したい方は弊社のブログ記事、Google ColaboratoryでDriveからデータを落とす方法を参考にすると良いかもしれません。
# Google Colaboratory用
from google.colab import drive
drive.mount('/content/drive')Mounted at /content/drive# Google Colaboratory用
import pandas as pd
df = pd.read_csv('/content/drive/My Drive/DDM_chap3/alcohol.csv')作成したデータフレームdfを確認してみると、NAのみの余分な行が含まれていたのでそれらを削除しました。
df.dropna(axis=0, how='any', inplace=True)次に列名を英語にしました。
columns_list = ['date', 'amount', 'TVCM', 'paper', 'OOH', 'WEB']
df.columns = columns_list
df.head()| date | amount | TVCM | paper | OOH | WEB | |
|---|---|---|---|---|---|---|
| 0 | 2015/9/7 | 5,554,981 | 58.86750 | 20340000.0 | 5890000.0 | 23,080 |
| 1 | 2015/9/14 | 6,071,669 | 235.18125 | 15470000.0 | 5740000.0 | 29,979 |
| 2 | 2015/9/21 | 5,798,657 | 252.18375 | 8325000.0 | 0.0 | 23,784 |
| 3 | 2015/9/28 | 6,235,157 | 75.25500 | 0.0 | 0.0 | 26,732 |
| 4 | 2015/10/5 | 6,861,105 | 0.00000 | 0.0 | 0.0 | 28,823 |
列名の意味は
date:日付
amount:缶アルコール飲料の売り上げ本数
TVCM:TVCMの延べ視聴率
paper:紙媒体の出稿金額
OOH:屋外広告や交通広告の出稿金額
WEB:WEB広告のクリック数
です。
plotメソッドとbarメソッドで折れ線グラフと棒グラフを作成
本の中でExcelを用いて行われている操作をPythonでやっていきましょう。可視化の際に用いられるライブラリとして有名なものの一つにmatplotlibがあります。苦手意識のある方はこちらの記事もあわせて読むと良いでしょう。barメソッドを用いて棒グラフを描く方法を紹介しています。
3-1. 折れ線グラフで各変数の形をチェック
まずは横軸が日付('date')、縦軸が缶アルコール飲料の売り上げ本数('amount')であるような折れ線グラフを描いてみます。ここでの注意点は、'amount'列の数値がカンマを含む文字列型になっていることです。
df.amount0 5,554,981
1 6,071,669
2 5,798,657
3 6,235,157
4 6,861,105
...
100 9,382,929
101 6,424,589
102 5,308,052
103 5,637,103
104 6,250,997
Name: amount, Length: 105, dtype: object文字列型の列を数値にしたいときはastypeメソッドを使うと良いのですが、カンマが含まれているとうまくいきません。例えば今回、df.amount.astype('int')とするとValueError: could not convert string to float: '5,554,981 'と出力されてしまいます。そこで、まずapplyメソッドを用いて、カンマを空白に置き換えます。以下を参考にしました。
df.amount = df.amount.apply(lambda x: x.replace(',','')).astype('int') # カンマを空白に置き換え、str型からint型にimport matplotlib.pyplot as plt
plt.figure(figsize=(25,10))
plt.plot(df['date'], df['amount'] )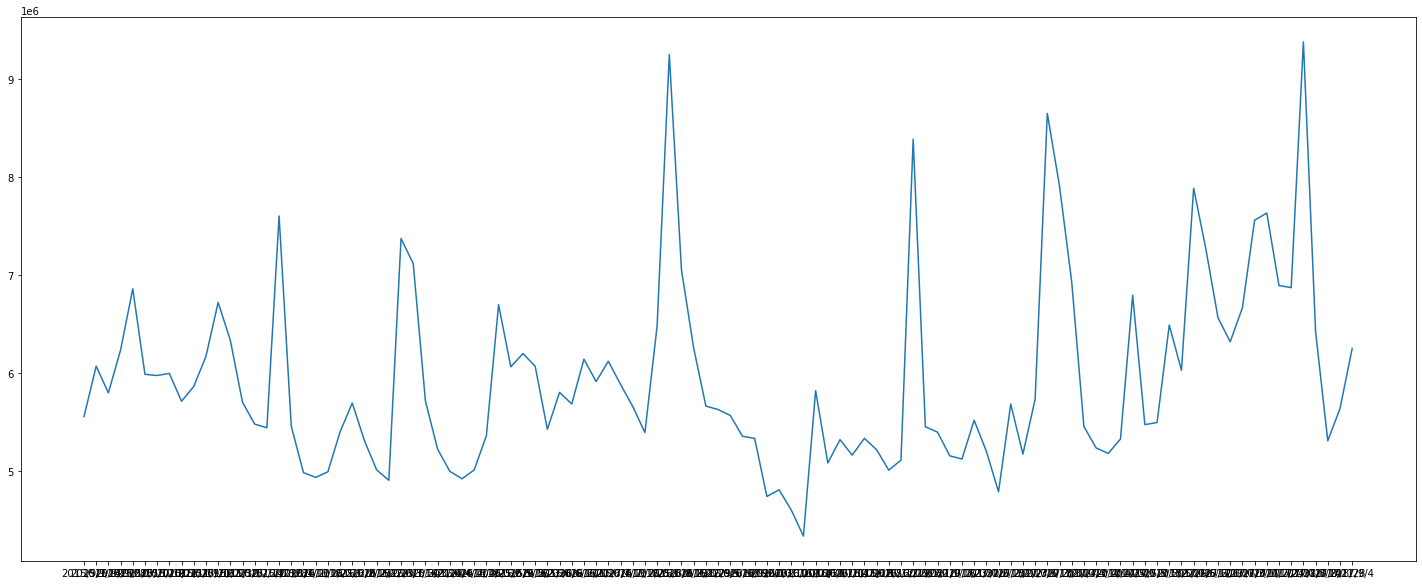
このままでは横軸の文字が小さくて見えないので、一部だけ表記することにしました。
xlist = df.date[::10] # date列の日付を10個刻みで取り出す
plt.figure(figsize=(25,10))
plt.plot(df['date'], df['amount'])
plt.xticks(ticks=xlist, labels=xlist) # 10週間隔で横軸の目盛りを表示
plt.show()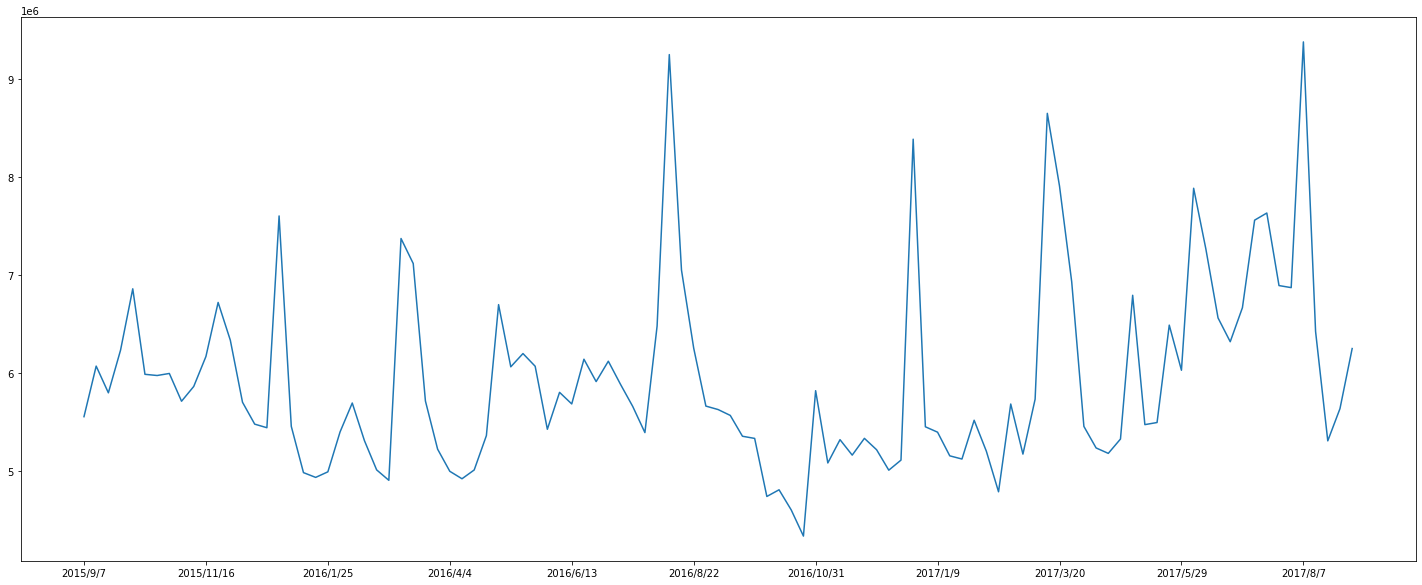
次に、横軸が日付('date')、縦軸がTVCMの延べ視聴率('TVCM')であるような棒グラフを描きます。
plt.figure(figsize=(25,10))
plt.bar(df['date'], df['TVCM'], color='orange')
plt.xticks(ticks=xlist, labels=xlist)
plt.show()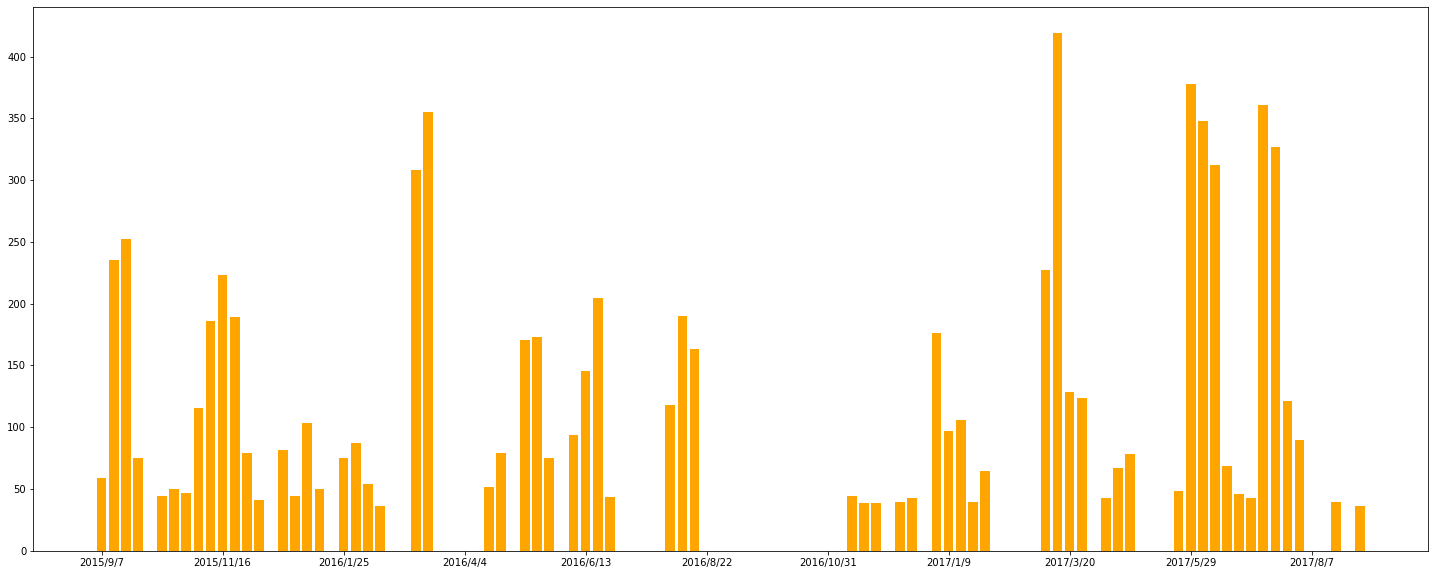
折れ線グラフと棒グラフをそれぞれ描くことができました。次に二つのグラフを一つにまとめます。
#xlist = df.date[::10] # 既出
plt.figure(figsize=(25,10))
plt.plot(df['date'], df['amount'])
plt.bar(df['date'], df['TVCM'], color='orange')
plt.xticks(ticks=xlist, labels=xlist)
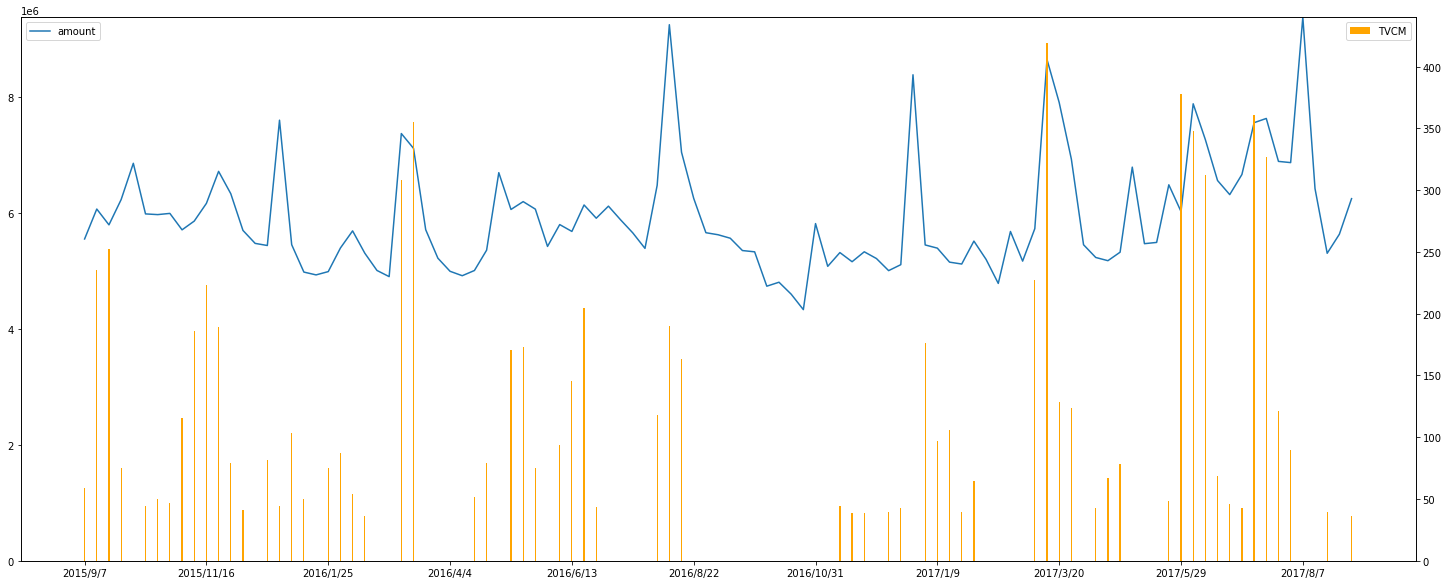
plt.show()これでは棒グラフが見えなくなってしまいます。そこで左右で異なる縦軸を用意し、グラフを描画します。以下を参考にしました。
ax とは何だ、という方は以下もご覧になると良いかもしれません。
fig, ax1 = plt.subplots(figsize=(25,10)) # Figureオブジェクトとそれに属する一つのAxesオブジェクト
ax2 = ax1.twinx() # twinx関数で二つのAxesオブジェクトを関連付け
# グラフの描画
ax1.plot(df['date'], df['amount'], label='amount')
ax2.bar(df['date'], df['TVCM'], color='orange', width=0.1, label='TVCM')
# ラベル付けや凡例
ax1.set_xticks(xlist) # グラフのラベル付け
ax1.set_xticklabels(xlist) # x軸のラベル付け
#fig.legend(['amount', 'TVCM'], loc='best') # 凡例
ax1.legend(loc=2) # 左上に凡例
ax2.legend(loc=1) # 右上に凡例
ax1.set_ylim([0, df['amount'].max()]) # 縦軸の範囲を調整(0.0, 9382929.0)
3-2 基本統計量とヒストグラムを使ってデータの形をチェック
基本統計量
先ほどのデータの基本統計量を確認します。本ではamount列のみに注目していますが、ここではすべての列について求めてみましょう。describeメソッドを用いて得られる基本統計量を確認してみると次のようになります。
df.describe()| amount | TVCM | paper | OOH | |
|---|---|---|---|---|
| count | 1.050000e+02 | 105.000000 | 1.050000e+02 | 1.050000e+02 |
| mean | 5.937047e+06 | 78.964643 | 8.101143e+06 | 3.136000e+06 |
| std | 9.661499e+05 | 101.784009 | 1.255423e+07 | 5.773868e+06 |
| min | 4.335326e+06 | 0.000000 | 0.000000e+00 | 0.000000e+00 |
| 25% | 5.309995e+06 | 0.000000 | 0.000000e+00 | 0.000000e+00 |
| 50% | 5.685093e+06 | 44.422500 | 7.175000e+06 | 0.000000e+00 |
| 75% | 6.320607e+06 | 105.630000 | 1.327000e+07 | 5.740000e+06 |
| max | 9.382929e+06 | 419.028750 | 1.085300e+08 | 2.785000e+07 |
WEB列がないのは、数値ではなく文字列型になっているからです。amount列と同様に変換してから再度describeメソッドを使ってみましょう。
df.WEB = df.WEB.apply(lambda x: x.replace(',','')).astype('int') df.describe()| amount | TVCM | paper | OOH | WEB | |
|---|---|---|---|---|---|
| count | 1.050000e+02 | 105.000000 | 1.050000e+02 | 1.050000e+02 | 105.000000 |
| mean | 5.937047e+06 | 78.964643 | 8.101143e+06 | 3.136000e+06 | 37823.323810 |
| std | 9.661499e+05 | 101.784009 | 1.255423e+07 | 5.773868e+06 | 16465.047521 |
| min | 4.335326e+06 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 17721.000000 |
| 25% | 5.309995e+06 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 28823.000000 |
| 50% | 5.685093e+06 | 44.422500 | 7.175000e+06 | 0.000000e+00 | 33106.000000 |
| 75% | 6.320607e+06 | 105.630000 | 1.327000e+07 | 5.740000e+06 | 39689.000000 |
| max | 9.382929e+06 | 419.028750 | 1.085300e+08 | 2.785000e+07 | 117831.000000 |
ここで得られた結果と本を比較してみると、不足しているのは標準誤差、最頻値、分散、尖度、歪度、範囲、合計です。これらも求めてみます。
import math
import pandas as pd
df1 = df.describe()
# 標準誤差
df_tmp = df1[2:3] / math.sqrt(len(df))
df_tmp.index = ['SE']
df1 = pd.concat([df1, df_tmp], axis=0)
# 分散
df_tmp = df1[2:3].apply(lambda x: x*x)
#df_tmp = pd.DataFrame(df.var(ddof=1)).T
df_tmp.index = ['var']
df1 = pd.concat([df1, df_tmp], axis=0)
# 尖度
df_tmp = pd.DataFrame(df.kurtosis()).T
df_tmp.index = ['kurtosis']
df1 = pd.concat([df1, df_tmp], axis=0)
# 歪度
df_tmp = pd.DataFrame(df.skew()).T
df_tmp.index = ['skew']
df1 = pd.concat([df1, df_tmp], axis=0)
# 範囲
df_tmp = pd.DataFrame(df1.apply(lambda x: x[7] - x[3])).T
df_tmp.index = ['range']
df1 = pd.concat([df1, df_tmp], axis=0)
# 合計
#columns_list = ['date', 'amount', 'TVCM', 'paper', 'OOH', 'WEB'] # 既出
df_tmp = pd.DataFrame(df[columns_list[1:]].sum()).T
df_tmp.index = ['sum']
df1 = pd.concat([df1, df_tmp], axis=0)
df1| amount | TVCM | paper | OOH | WEB | |
|---|---|---|---|---|---|
| count | 1.050000e+02 | 105.000000 | 1.050000e+02 | 1.050000e+02 | 1.050000e+02 |
| mean | 5.937047e+06 | 78.964643 | 8.101143e+06 | 3.136000e+06 | 3.782332e+04 |
| std | 9.661499e+05 | 101.784009 | 1.255423e+07 | 5.773868e+06 | 1.646505e+04 |
| min | 4.335326e+06 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 1.772100e+04 |
| 25% | 5.309995e+06 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 2.882300e+04 |
| 50% | 5.685093e+06 | 44.422500 | 7.175000e+06 | 0.000000e+00 | 3.310600e+04 |
| 75% | 6.320607e+06 | 105.630000 | 1.327000e+07 | 5.740000e+06 | 3.968900e+04 |
| max | 9.382929e+06 | 419.028750 | 1.085300e+08 | 2.785000e+07 | 1.178310e+05 |
| SE | 9.428657e+04 | 9.933102 | 1.225168e+06 | 5.634718e+05 | 1.606824e+03 |
| var | 9.334456e+11 | 10359.984557 | 1.576088e+14 | 3.333755e+13 | 2.710978e+08 |
| kurtosis | 2.175782e+00 | 1.959914 | 3.911519e+01 | 6.875505e+00 | 5.557317e+00 |
| skew | 1.392248e+00 | 1.609215 | 5.135276e+00 | 2.436260e+00 | 2.107262e+00 |
| range | 5.047603e+06 | 419.028750 | 1.085300e+08 | 2.785000e+07 | 1.001100e+05 |
| sum | 6.233899e+08 | 8291.287500 | 8.506200e+08 | 3.292800e+08 | 3.971449e+06 |
# ユニーク件数
print('ユニーク件数(amount):' + str(len(df['amount'].unique())))
print('ユニーク件数(TVCM):' + str(len(df['TVCM'].unique())))
print('ユニーク件数(paper):' + str(len(df['paper'].unique())))
print('ユニーク件数(WEB):' + str(len(df['WEB'].unique())))
# 最頻値
df_tmp = df[['TVCM', 'paper']].mode()
df_tmpユニーク件数(amount):105
ユニーク件数(TVCM):65
ユニーク件数(paper):60
ユニーク件数(WEB):105| TVCM | paper | |
|---|---|---|
| 0 | 0.0 | 0.0 |
最頻値は不要でしょうが、一応付け加えておきました。
ヒストグラム
次に、amount列のヒストグラムを描きます。データ区間は本と少し異なりますが、区間が11個である点は合わせました。
import pandas as pd
import matplotlib.pyplot as plt
plt.figure(figsize=(25,10))
frequency, bin, histogram = plt.hist(df['amount'], bins=11)
plt.xticks(ticks=bin, labels=bin)
plt.xlabel('period')
plt.ylabel('count')
plt.title('histogram')
plt.legend(['count'], loc='best') # 凡例
print('データ区間の上限 : ' + str(bin[1:]))
print('頻度:' + str(frequency))
plt.show()データ区間の上限 : [4794199. 5253072. 5711945. 6170818. 6629691. 7088564. 7547437. 8006310.
8465183. 8924056. 9382929.]
頻度:[ 4. 21. 30. 19. 10. 9. 3. 5. 1. 1. 2.]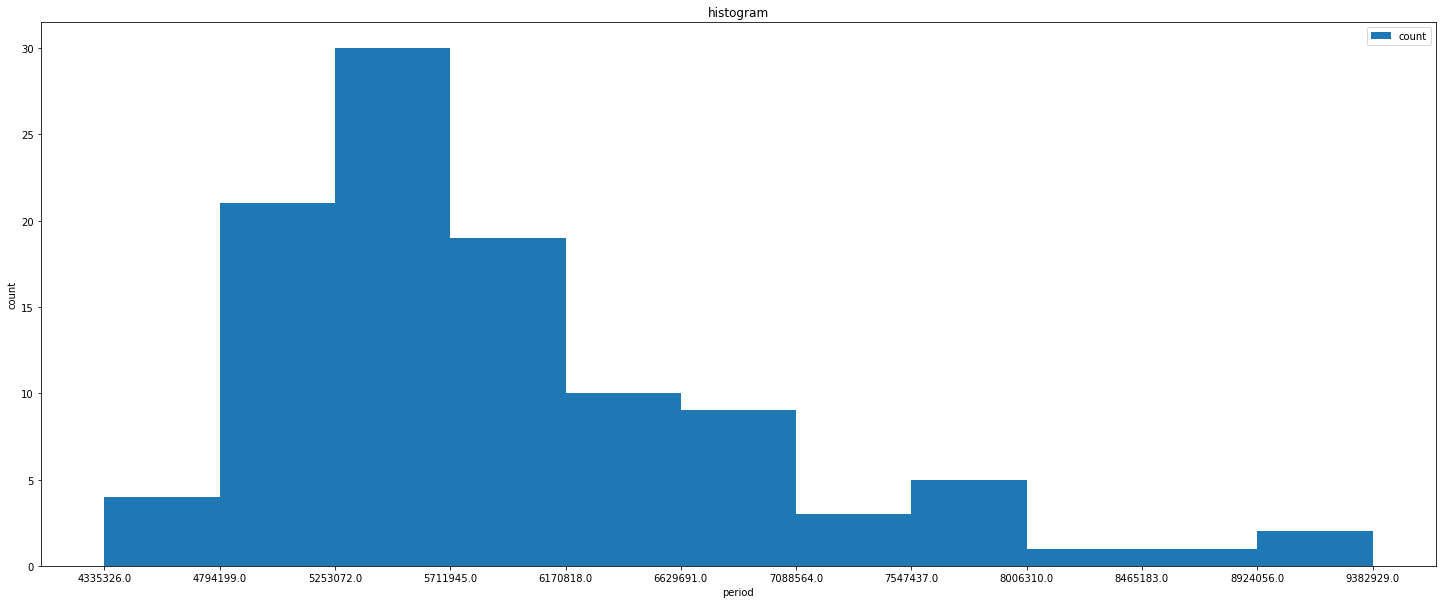
3-3 データの形のチェック(まとめ)
ここには問題の掲載はなく、3-1, 3-2 のまとめのみ書いてありました。
まとめ
前編はここまでとします。後編では相関係数や季節性をテーマにします。


