
Propehtとは
ProphetはFacebookが公開してるライブラリで、簡単に時系列予測が行え、結果がトレンドや季節性など構造化して得られるので可読性に優れているとも言われています。
Prophetにより予測を行ってみる
Prophetがどのようなモデルなのか説明する前に、非常に簡単に使えるためまずは使ってみましょう。
# ライブラリの読み込み
import pandas as pd
from fbprophet import Prophet
import matplotlib.pyplot as plt月ごとの飛行機の乗車数についてのデータを利用します。
こちらからダウンロードしました。
data = pd.read_csv('path')
data.head()| Month | #Passengers | |
|---|---|---|
| 0 | 1949-01 | 112 |
| 1 | 1949-02 | 118 |
| 2 | 1949-03 | 132 |
| 3 | 1949-04 | 129 |
| 4 | 1949-05 | 121 |
prophetでは時間のcolum名をds、目的変数のcolum名をyとする必要があるので変更します。
data.columns = ['ds','y']
data.head()| ds | y | |
|---|---|---|
| 0 | 1949-01 | 112 |
| 1 | 1949-02 | 118 |
| 2 | 1949-03 | 132 |
| 3 | 1949-04 | 129 |
| 4 | 1949-05 | 121 |
#前半100個を利用
data_train = data[:100]今回は月ごとのデータなので週、日ごとの季節性についてはFalseにしてあります。
m = Prophet(weekly_seasonality=False,daily_seasonality=False)
m.fit(data_train)make_future_dataframeを用いることで学習データに予測したい期間を加えた時間が得られます。
future = m.make_future_dataframe(periods=len(data_test),freq='M')
future| ds | |
|---|---|
| 0 | 1949-01-01 |
| 1 | 1949-02-01 |
| 2 | 1949-03-01 |
| 3 | 1949-04-01 |
| 4 | 1949-05-01 |
| … | … |
| 139 | 1960-07-31 |
| 140 | 1960-08-31 |
| 141 | 1960-09-30 |
| 142 | 1960-10-31 |
| 143 | 1960-11-30 |
144 rows × 1 columns
予測を行います。
予測結果はデータフレームで得られ、必要な情報が各種関数で可視化できます。
predict = m.predict(future)
predict.head()| ds | trend | yhat_lower | yhat_upper | trend_lower | ・・・ | yhat | |
|---|---|---|---|---|---|---|---|
| 0 | 1949-01-01 | 110.704240 | 76.896936 | 110.412871 | 110.704240 | ・・・ | 94.182651 |
| 1 | 1949-02-01 | 112.751002 | 73.569810 | 107.970519 | 112.751002 | ・・・ | 90.573166 |
| 2 | 1949-03-01 | 114.599690 | 106.469888 | 139.859590 | 114.599690 | ・・・ | 122.605733 |
| 3 | 1949-04-01 | 116.646452 | 98.748975 | 131.227418 | 116.646452 | ・・・ | 115.763640 |
| 4 | 1949-05-01 | 118.627189 | 97.239853 | 131.585167 | 118.627189 | ・・・ | 115.075401 |
予測で得られた平均値と標準偏差を描画します。
fig1 = m.plot(predict)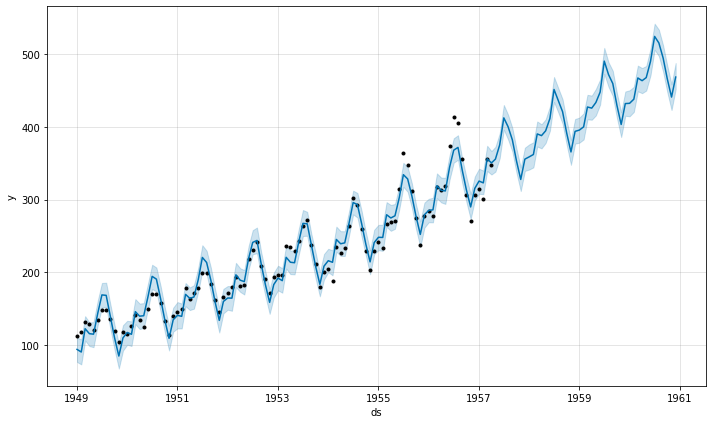
トレンドと季節性に分けて、描画します。
今回は年周期のみを適用しているのでトレンドと年の季節性に分解されています。
fig2 = m.plot_components(predict)
最後に実際のデータと予測値を比較します。
plt.figure(figsize=(12,6))
plt.plot(data.y,label = 'True')
plt.plot(predict.yhat,label='Predict')
plt.legend()
トレンドについては当てられているが、季節性の変化が捕らえられていない様子ですね。
Prophetモデル解説
Prophetを使って時系列予測を行なってみました。
以降はProphetが利用しているモデルについて簡単に説明してみます。
Prophetは次のような時系列モデルを利用しています。
y(t) = g(t) + s(t) + h(t) + \epsilon_t
g(t)はトレンド、s(t)は季節性、h(t)は祝日などのイベント効果を表しています。
このように時系列の要素ごとにモデリングしているため上記で可視化したようにトレンドと季節性を分けて考えることができます。
また、ARIMAやVARのような自己回帰ではなく時間を引数にとるモデルとなっています。
ではそれぞれg(t),s(t),h(t)について見ていきます。
トレンド項 g(t)
g(t)は線形トレンド、上限を持つトレンドの2通りがあります。
まずは線形トレンドについて説明します。
基本形としては
g(t) = kt + m
という線形モデルを考えます。次にトレンドの変化を考慮した場合を考えます。
s = (s_1,s_2,...,s_S)のようにトレンドが変化する時刻が与えられた時に
トレンドの変化量を表すベクトル\delta = (\delta_1,...,\delta_S)とすると
g(t) = (k+a(t)^T\delta)t + (m + a(t)^T\gamma)
となります。
\gammaはトレンドの変化で変化した切片を調整するベクトルになります。
\gamma_j = -s_j*\delta_j上限を持つトレンドは
g(t) = \frac{C(t)}{1 + \exp(-(k+a(t)^T\delta)(t - (m + a(t)^T\gamma)))}
として上限がC(t)になるように設計されます。
\gamma_j = \left(s_j - m - \sum_{l < j}\gamma_l\right)\left(1-\frac{k + \sum_{l < j}\delta_l}{k + \sum_{l < j} \delta_l}\right)季節性項 s(t)
s(t)はフーリエ級数により表現され、Pの周期を持ち、振幅、振動数が異なる並みの足し合わせとなります。
s(t) = \sum_{n=1}^N a_n \cos\left(\frac{2\pi nt}{P}\right) +b_n \sin\left(\frac{2\pi nt}{P}\right)
Pは周期を表します。週の場合はP=7となります。
AICなどの情報量基準を用いてハイパーパラメータとなるNを最適化することも可能です。
Prophetの論文中では、年周期の場合はN=10、週周期の場合はN=3とすると多くの問題で上手くいくと書かれています。
また、パラメータlatex^T[/latex]の事前分布をNormal(0,\sigma^2)とします。
イベント項 h(t)
h(t)は次のように表されます。
h(t) = Z(t)k
Z(t)はイベントiが起った時にZ(t)_i = 1となるベクトルで、kは係数ベクトルで、事前分布はNormal(0,\nu^2)とします。
パラメータ推定
パラメータ推定はMAP推定を利用します。
モデルy(t) = g(t) + s(t) + h(t) + \epsilon_tは
g(t)での初期係数k,m、トレンド変化\delta、
s(t)でのa_i,b_i、
h(t)でのk
をそれぞれパラメータに持ち、MAP推定を用いてこれらのパラメータ推定を行います。
ProphetではStanを利用してMAP推定を行なっており、論文中に次のようにモデルが書かれています。

モデルは論文より引用しました。


