「構造変化」を伴う時系列データを状態空間モデルを用いて分析してみたいと思います。まずはこちらのデータをご覧ください。

これはRの組み込みデータNileで、ナイル川の年間流水量が記録されています。パッと見は不規則な変動が続いていてこれといった特徴は見えません。しかし、歴史的事実として1899年にアスワン・ダムが建設され流水量が急減した、ということがわかっています。このような構造変化を状態空間モデルで表現していきましょう。手法として時変カルマンフィルタとMCMCを紹介しますが、最終的にMCMCによって状態に「いつ」「どの程度」の変化が生じたのかを視覚的に表すことができます。なお、今回の内容は基礎からわかる時系列分析 (技術評論社)12章を参考にしています。
0.時不変カルマンフィルタ
まずは何も工夫せずにローカルレベルモデルでモデリングしていきます。ローカルレベルモデルはRのdlmライブラリを用いることで簡単に実装できます。
#---
# 0.時不変カルマンフィルタ(ローカルレベル)----
#---
library(dlm)
set.seed(123)
y = Nile
t_max = length(y)
# モデルの定義
build_dlm = function(par){
return(
dlmModPoly(order = 1, dW = exp(par[1]), dV = exp(par[2]))
)
}
# パラメータの最尤推定
fit_dlm = dlmMLE(y = y, parm = c(0,0), build = build_dlm)
# パラメータの最尤推定結果を代入
mod = build_dlm(fit_dlm$par)
# フィルタリング
dlmFiltered_obj = dlmFilter(y = Nile, mod = mod)
# 平滑化
dlmSmoothed_obj = dlmSmooth(y = Nile, mod = mod)
# 平滑化分布の平均と標準偏差を求める
s = dropFirst(dlmSmoothed_obj$s)
s_sdev = sqrt(
dropFirst(as.numeric(
dlmSvd2var(dlmSmoothed_obj$U.S, dlmSmoothed_obj$D.S)
))
)
# 平滑化分布の2.5%値と97.5%値を求める
s_quant = list(s + qnorm(0.025, sd = s_sdev), s + qnorm(0.975, sd = s_sdev))
# 結果のプロット
ts.plot(cbind(Nile, s, do.call('cbind', s_quant)),
main = '時不変カルマンフィルタの平滑化分布',
col = c('lightgray', 'black', 'black', 'black'),
lty = c('solid', 'solid', 'dashed', 'dashed'))
legend(legend = c('観測値', '平均(平滑化)', '95%区間'),
lty = c('solid', 'solid', 'dashed'),
col = c('lightgray', 'black', 'black'),
x = 'topright')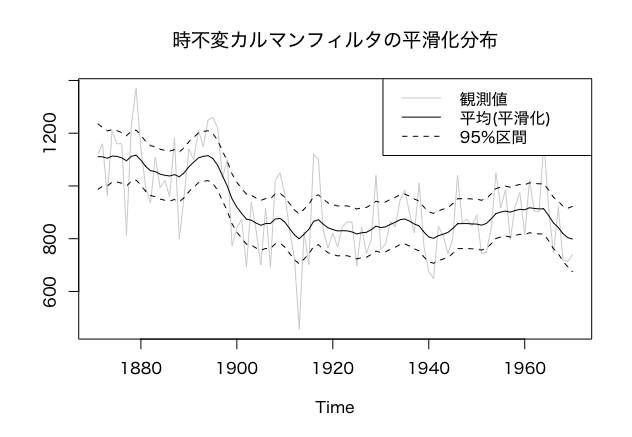
時不変カルマンフィルタによる平滑化分布は上のようになりました。1899年の急変にはいまいち追従できていません。ここからは、先見情報を活用する時変カルマンフィルタと急変があった時期も併せて推測するMCMCを実装して分析を改善していきます。
1.時変カルマンフィルタ
時変カルマンフィルタの「時変」とは、ノイズの分散が各時点ごとに異なる、という意味です。ここでは変化点を既知として、1899年のシステムノイズだけ分散の大きい正規分布に従うこととします。
#---
# 2.時変カルマンフィルタ(ローカルレベル、変化点既知)----
#---
set.seed(123)
y = Nile
t_max = length(y)
# モデルの定義
build_dlm = function(par){
tmp = dlmModPoly(order = 1, dV = exp(par[1]))
tmp$JW = matrix(1, nrow = 1, ncol = 1) # p278下を読むこと
tmp$X = matrix(exp(par[2]), nrow = t_max, ncol = 1)
j = which(time(y) == 1899)
tmp$X[j, 1] = tmp$X[j, 1] * exp(par[3])
return(tmp)
}
# パラメータの最尤推定
fit_dlm = dlmMLE(y = y, parm = rep(0,3), build = build_dlm)
# パラメータの最尤推定結果を代入
modtv = build_dlm(fit_dlm$par)
as.vector(mod$X); mod$V
# フィルタリング
dlmFiltered_obj = dlmFilter(y = Nile, mod = modtv)
# 平滑化
dlmSmoothed_obj = dlmSmooth(y = y, mod = modtv)
# 平滑化分布の平均と標準偏差を求める
stv = dropFirst(dlmSmoothed_obj$s)
# 結果のプロット
ts.plot(cbind(Nile, stv),
main = '時変カルマンフィルタの平滑化分布',
col = c('lightgray', 'black', 'black', 'black'),
lty = c('solid', 'solid', 'dashed', 'dashed'))
legend(legend = c('観測値', '平均(平滑化)', '95%区間'),
lty = c('solid', 'solid', 'dashed'),
col = c('lightgray', 'black', 'black'),
x = 'topright')関数build_dlmについて詳しく解説します。この関数の中ではまずdlmModPoly()でローカルレベルモデルのテンプレートtmpを作っています。続いてシステムノイズの分散を考慮するため、tmp$JWに行列1を設定します。分散の具体的な値はtmp$Xの一列目に格納することになるため、一旦全時点にベースとなる時不変の値を一律に設定し、1899年だけに正の倍率を許容します。こうして作成したモデルに対しパラメータを最優推定し、平滑化を行ったところ、結果は次のようになりました。
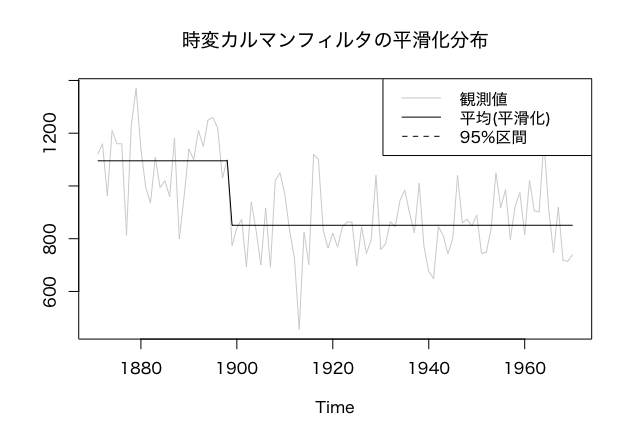
1899年の急変の鋭く追従していますね。このように、いつ変化が起こったのかわかっている場合には、時変カルマンフィルタによって変化を観察することができます。
2. MCMC
ここでは一般状態空間モデルによって構造変化を表現します。具体的には、システムノイズに馬蹄分布(正規分布の尺度混合。裾が厚く峰への集中度が高い。)を仮定することで「まれに起きる構造変化」も考慮することができるようにします。馬蹄分布は条件付きで線形ガウス状態空間モデルとなることを用いて、状態変数の事後分布からのサンプリングを行います。
Stanのコードは以下の通りです。条件付きでカルマンフィルタの全時点尤度を計算するモデルです。尤度の計算式については以下にまとめたので参照ください。
// locallevel.stan
// functionはこちら参照:https://raw.githubusercontent.com/jrnold/dlm-shrinkage/master/stan/includes/dlm.stan
functions{
vector dlm_local_level_loglik(int n,
vector y, int[] miss,
vector V, vector W,
real m0, real C0){
/*
各時点についてカルマンフィルタ(ローカルモデル)の対数尤度を計算する関数。
Wが時変なので初めから全時間の対数尤度を計算することはできず、対数尤度のベクトルを返す。
<input>
n:時系列長(t_max)
y:観測データ(n次元ベクトル)
miss:欠損の指標(int箱)
V:全時点分の観測ノイズ (n次元ベクトル)
W:全時点分の状態ノイズ (n次元ベクトル)
m0:状態の事前分布の平均値
C0:状態の事前分布の分散
<output>
対数尤度のベクトル(あとで和を取る)
*/
// 状態の事前分布 p(x)
real a; // 平均
real R; // 分散
// t時点での尤度関数 p(theta | y)
real f; // 予測誤差の平均
real Q; // 予測誤差の分散
real Q_inv;
// 状態の事後分布 p(x | y)
real m;
real C;
// 予測誤差
real e;
// カルマンゲイン
real K;
// データn個の尤度
vector[n] loglik;
m = m0;
C = C0;
for (t in 1:n){
// 逐次予測
a = m;
R = C + W[t];
m = a;
C = R;
if (int_step(miss[t])){ // t番目が欠損の場合
e = 0.0;
Q_inv = 0.0;
}else{ // 欠損でない場合
f = m;
Q = C + V[t];
Q_inv = 1.0 / Q;
e = y[t] - f;
K = C * Q_inv;
m = m + K * e;
C = C - pow(K, 2) * Q;
loglik[t] = - 0.5 * (log(2 * pi()) + log(Q) + pow(e, 2) * Q_inv);
}
}
return loglik;
}
}
data{
int<lower = 1> t_max; // 時系列長
vector[t_max] y; // 観測値
int miss[t_max]; // 欠損値の指標
real m0; // 事前分布の平均
real<lower = 1> C0; // 事前分布の分散
}
parameters{
vector<lower = 0>[t_max] lambda; // 状態ノイズの標準偏差(時変の倍率)
real<lower = 0> W_sqrt; // 状態ノイズの標準偏差(時不変のベース)
real<lower = 0> V_sqrt; // 観測ノイズの標準偏差
}
transformed parameters{ // パラメータをdlm_local_level_loglikに整合させる
vector[t_max] W; // 状態ノイズの分散 (時変)
vector[t_max] V; // 観測ノイズの分散 (時不変)
real log_lik; // 全時点分の対数尤度
for (t in 1:t_max){
W[t] = pow(lambda[t] * W_sqrt, 2); // 状態ノイズの分散(powは二乗)
}
V = rep_vector(pow(V_sqrt, 2), t_max); // 観測ノイズの分散(rep_vectorでベクトルを並べる)
log_lik = sum(dlm_local_level_loglik(t_max, y, miss, V, W, m0, C0));
}
model{
target += log_lik;
lambda ~ cauchy(0,1);
}
Stanコードを実行するためのRのコードは次の通りです。
library(rstan)
set.seed(123)
y = Nile
t_max = length(y)
# 呪文
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
theme_set(theme_get() + theme(aspect.ratio = 3/4))
# モデルの生成、コンパイル
stan_mod_out = stan_model(file = 'LocalLevel.stan')
# 平滑化
fit_stan = rstan::sampling(object = stan_mod_out,
data = list(t_max = t_max, y = y,
miss = as.integer(is.na(y)),
m0 = mod$m0, C0 = mod$C0[1,1]),
pars = c('lambda', 'W_sqrt', 'V_sqrt'),
seed = 123)
# 結果の確認
oldpar = par(no.readonly = TRUE); options(max.print = 99999)
print(fit_stan, probs = c(0.025, 0.5, 0.975))
options(oldpar)
traceplot(fit_stan, pars = c('W_sqrt', 'V_sqrt'), alpha = 0.5)
# カルマンフィルタのモデルをコピーして修正
mod_MCMC = modtv
mod_MCMC$X[,1] = (summary(fit_stan)$summary[1:100, 'mean'] *
summary(fit_stan)$summary['W_sqrt', 'mean']) ^ 2
mod_MCMC$V[1,1] = (summary(fit_stan)$summary['V_sqrt', 'mean']) ^ 2
# カルマン平滑化
dlmSmoothed_obj = dlmSmooth(y = y, mod = mod_MCMC)
# 平滑化分布の平均
stv_MCMC = dropFirst(dlmSmoothed_obj$s)
# プロット
ts.plot(cbind(y, stv_MCMC),
main = '時変MCMCの平滑化分布',
lty = c('solid', 'solid'),
col = c('lightgray', 'black'))
legend(legend = c('観測値', '平均(平滑化)'),
lty = c('solid', 'solid'),
col = c('lightgray', 'black'),
x = 'topright')
Rでfit_stanを表示させることでマルコフ連鎖の収束を確認することができます。今回は実効サンプルサイズ、R^hatともに良い値となっていました。またトレースプロットは以下の通りで、推定結果がきちんと混ざっていることも確認できます。
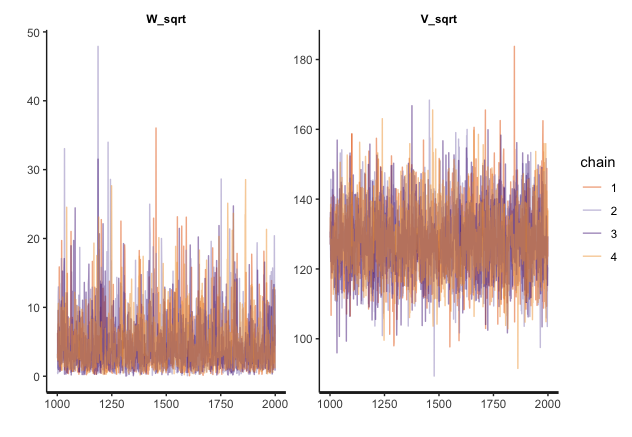
最後に状態の平滑化分布を時変カルマンフィルタを用いて求めています。この際、時変モデルmod_tvをmod_MCMCに一旦コピーして、システムノイズの時変分散が入るXと観測ノイズの分散が入るVにMCMCで推定した平均値をプラグインしています。平滑化分布の平均値をプロットしたものが以下の通りです。
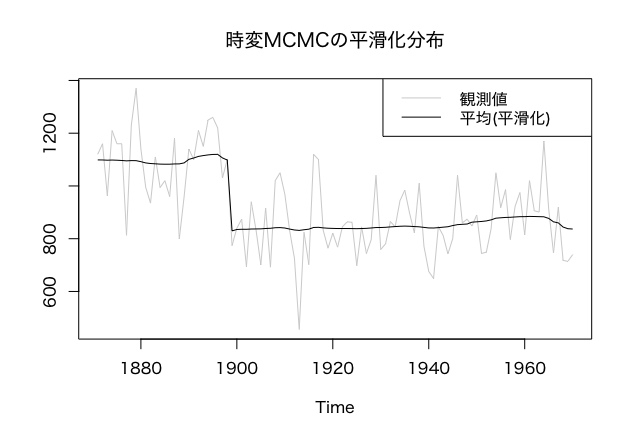
1899年の急変に鋭く追従できています。
番外(macでStanの環境構築)
今回の実装ではStanを用いるのでmacでインストールする方法についてこちらを参考に解説します。C++の環境が整っていない方はxcodeをApp Storeからインストールしてください。
正直私も何をやっているかをちゃんと理解しているわけではなく、呪文を唱えたらうまくいった程度の感覚なのでやり方の一例として参考にしてください。
- Rで次のように入力します。
remove.packages("rstan")
if (file.exists(".RData")) file.remove(".RData")- Rのバージョンを確認します。記事執筆時点での最新バージョンは4.xです。3.x以前になっているとやり方が変わってくるようなので可能であればアップデートしましょう。
version # 3.x以降であればOK- Rで次のように入力します。実行に時間がかかります。
install.packages("rstan", repos = "https://cloud.r-project.org/", dependencies = TRUE)- 3.でエラーになってしまったので、指示通りコマンドラインでディレクトリを削除します。
$ rm -rf /Library/Frameworks/R.framework/Versions/4.0/Resources/library/00LOCK-rstan
- Rで次のコードが正常に実行できればインストール完了です。
example(stan_model, package = "rstan", run.dontrun = TRUE) 3. おわりに
今回は時変カルマンフィルタとMCMCによって構造変化を伴う時系列データを分析する手法を紹介しました。「介入と非介入の二群を用意することはできなかったけど介入前後の時系列データはある」といった時に介入効果を可視化する、といった応用ができそうです。最後までお読みいただきありがとうございました。