今回は、前回に引き続きPythonを使った時系列分析を行います。前回の記事はこちらです。
前回の記事ではデータのトレンドと季節性を分析し、データの定常性についての検定までを行いました。今回の記事では前回の記事で分析したデータの特徴を取り入れたモデルを推定していきます。

SARIMAモデルの推定

まず、データを訓練データとテストデータに分けます。今回は2008年までのデータを訓練データにして、それ以外のデータをテストデータにします。

# 訓練データとテストデータに分ける
train = data[:"2008"]

それでは実際にモデルを推定していきます。今回は季節変動を考慮したSARIMAモデルで実装していきます。SARIMAモデルを推定する際に難しいのが複数のパラメータを適切に設定しなければいけない点です。まず一旦パラメータは適当に設定してモデルを推定してみます。

# パラメーターは適当
sarima_2_1_1_111 = sm.tsa.SARIMAX(train, order=(2,1,1), seasonal_order=(1,1,1,12)).fit()
print(sarima_2_1_1_111 .summary())

Statespace Model Results ==========================================================================================
Dep. Variable: shipments No. Observations: 108
Model: SARIMAX(2, 1, 1)x(1, 1, 1, 12) Log Likelihood -836.914
Date: Tue, 08 Oct 2019 AIC 1685.828 Time: 17:04:22 BIC 1701.921 Sample: 01-01-2000 HQIC 1692.353 - 12-01-2008
Covariance Type: opg ==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.0719 0.321 -0.224 0.823 -0.700 0.557 ar.L2 -0.0769 0.164 -0.470 0.639 -0.398 0.244 ma.L1 -0.4611 0.330 -1.398 0.162 -1.107 0.185 ar.S.L12 0.2114 0.628 0.337 0.736 -1.019 1.442 ma.S.L12 -0.3615 0.626 -0.577 0.564 -1.588 0.865 sigma2 2.266e+06 2.05e+05 11.049 0.000 1.86e+06 2.67e+06 ===================================================================================
Ljung-Box (Q): 38.69 Jarque-Bera (JB): 116.11 Prob(Q): 0.53 Prob(JB): 0.00 Heteroskedasticity (H): 1.19 Skew: -1.14 Prob(H) (two-sided): 0.62 Kurtosis: 7.91 ===================================================================================
Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step).

summary()でモデルの詳しい情報を見ることができます。ここにある「AIC」という値がモデルの当てはまりを評価する指標になっていて、AICが小さいほどモデルの当てはまりがいいといえます。

それでは次に、先ほど適当に指定したパラメータを適切なものにしてモデルの精度を上げていきます。手法は単純で、パラメータをとり得る範囲を定めたうえで総当たりでモデルを作成し、その中で一番AICが小さいものを採択します。

# 総当たりで、AICが最小となるSARIMAの次数を探す
max_p = 3
max_q = 3
max_d = 1
max_sp = 2
max_sq = 2
max_sd = 2
pattern = max_p*(max_q + 1)*(max_d + 1)*(max_sp + 1)*(max_sq + 1)*(max_sd + 1)
modelSelection = pd.DataFrame(index=range(pattern), columns=["order","season","aic"])
# 自動SARIMA選択
num = 0
for p in range(1, max_p + 1):
    for d in range(0, max_d + 1):
        for q in range(0, max_q + 1):
            for sp in range(0, max_sp + 1):
                for sd in range(0, max_sd + 1):
                    for sq in range(0, max_sq + 1):
                        sarima = sm.tsa.SARIMAX(
                            train, order=(p,d,q),
                            seasonal_order=(sp,sd,sq,12),
                            enforce_stationarity = False,
                            enforce_invertibility = False
                        ).fit()
                        modelSelection.ix[num]["order"] = (p, d, q)
                        modelSelection.ix[num]["season"] = (sp, sd, sq)
                        modelSelection.ix[num]["aic"] = sarima.aic
                        num = num + 1

上記のコードは計算に数十分かかることがあります。計算が終わったら以下のようにAICが最も低いパラメータを取り出すことができます。

# AIC最小モデル
modelSelection[modelSelection.aic == min(modelSelection.aic)]

それではこのパラメータを使ってモデルを推定してみます。

# AIC最小モデル
best_sarima = sm.tsa.SARIMAX(train, order=(3,1,1), seasonal_order=(2,2,1,12), enforce_stationarity = False, enforce_invertibility = False).fit()

推定したモデルの残差に有意な自己相関がないかを確かめるためにコレログラムを図示します。

# 残差のコレログラグラム
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(resid_best_sarima, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(resid_best_sarima, lags=40, ax=ax2)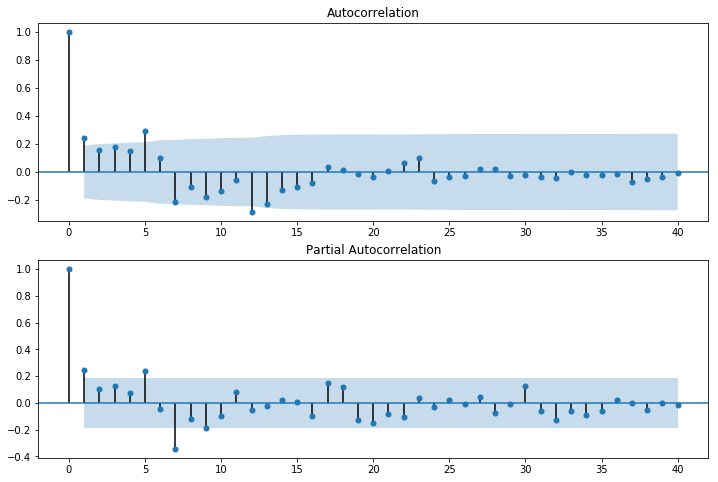

前半のラグのほうに有意な自己相関が残ってしまっていますが、その他の点は小さく収まっています。
最後に推定したモデルで予測をします。

# テストデータの範囲を予測
pred = best_sarima.predict('2008-01-01', '2009-12-01')
# 実データと予測結果の図示
fig = plt.figure(figsize=(10,5))
plt.plot(data)
plt.plot(pred, "r")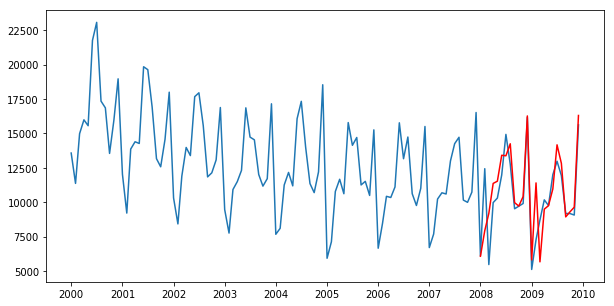

少し見にくいので、予測部分を拡大しています。

# 拡大
pointed_pred = best_sarima.predict('2008-01-01', '2009-12-01')
plt.plot(data["2008-01-01":])
plt.plot(pointed_pred, "r")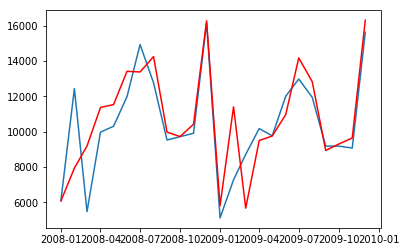

おおまかなグラフの形状はあっているように見えますが、2008年前半の例外的に販売量が多くなってしまっている部分がそのままモデルに反映されてしまっているように見えます。

今回は単変量の分析でしたが、他に説明変数を加えることでさらに精度の高いモデルの推定ができそうです。

最後に

いかがでしたか。今回は細かい説明は省きながらですが、Pythonを用いた時系列分析の一連の流れをご紹介しました。次回はもう少し細かい部分を深ぼってPythonを用いた時系列分析について書けたらと思います。