はじめに
本記事では、クラス分類のための人工データ発生について説明します。
今回は、Rのmvtnormを用いたコードについて記します。
また、そのデータについて散布図を用いて可視化を行います。
想定される読者
- Rで人工データを発生させたい方
mvtnormの使い方を知らない方ggplotで散布図を作成したい方
データ発生
本記事では、サンプルサイズをn、変数の次元をdとします。このとき、ある個体iの説明変数を\bm{x}_i\in\mathbb{R}^d (i=1,2,\cdots,n)とし、データ行列をX=(\bm{x}_1,\bm{x}_2,\cdots,\bm{x}_n)^Tとします(X \in \mathbb{R} ^ {n \times d})。そして、ある個体iは下記のように発生させます。
\bm{x}_i \sim \mathcal{N}_d(\bm{\mu}, \mathit{\Sigma})
ここで、\mathcal{N}_dはd次元の多変量正規分布(多変量ガウス分布)、\bm{\mu}\in\mathbb{R}^dはd次元の母平均ベクトル、\mathit{\Sigma}\in\mathbb{R}^{d\times d}はd\times dの母分散共分散行列を意味します。
今回の設定
今回は2クラスのデータを発生させます。多変量正規分布について上述しましたが、各クラスの母平均ベクトルと母分散共分散行列はこのように設定します。
クラス1: \bm{\mu}^{[1]}=(\mu_1,\mu_1,\cdots,\mu_1)^T\in\mathbb{R}^d, \mathit{\Sigma}^{[1]}=\sigma_1^2\times \begin{pmatrix}1 & \cdots & \rho_1 & \cdots & \rho_1 \\\vdots & \ddots & & & \vdots \\\rho_1 & & 1 & & \rho_1 \\\vdots & & & \ddots & \vdots \\\rho_1 & \cdots & \rho_1 & \cdots & 1\end{pmatrix}\in\mathbb{R}^{d\times d}
クラス2: \bm{\mu}^{[2]}=(\mu_2,\mu_2,\cdots,\mu_2)^T\in\mathbb{R}^d, \mathit{\Sigma}^{[2]}=\sigma_2^2\times \begin{pmatrix}1 & \cdots & \rho_2 & \cdots & \rho_2 \\\vdots & \ddots & & & \vdots \\\rho_2 & & 1 & & \rho_2 \\\vdots & & & \ddots & \vdots \\\rho_2 & \cdots & \rho_2 & \cdots & 1\end{pmatrix}\in\mathbb{R}^{d\times d}
各パラメータの簡単な説明を致します。
- 右上の[1],[2]は所属クラスを意味します。(右下の添え字で記しても良いのですが、x_iなどの文字と差別化を図るために、今回はこのように表記いたします。)
- 母平均ベクトル\bm{\mu}^{[1]},\bm{\mu}^{[2]}は、各要素にそれぞれ同じ値を設定しています。
- 母分散共分散行列\mathit{\Sigma}^{[1]},\mathit{\Sigma}^{[2]}は、\sigma^2\in\mathbb{R}を相関係数行列の全要素に掛けています。相関係数行列は、対角成分が1で、非対角成分が、\rho_1, \rho_2です。\sigma_1^2,\sigma_2^2は0以上の値で、\rho_1,\rho_2は0以上1以下の値とします。
より細かくモデルを設定することも可能ですが、今回は上記のように設定しました。
設定するパラメータ
これまでの計算式を基に、設定する必要があるパラメータに関して整理致します。
- サンプルサイズn: データの行数に該当します。
- 変数次元d: データの列数に該当します。
- クラス比: クラス間のサンプルサイズの比率です。
- 平均\mu_1,\mu_2: 母平均ベクトルの要素です。
- 相関\rho_1,\rho_2: 相関係数行列の非対角成分です。
- 分散\sigma_1,\sigma_2: 相関係数行列に掛ける値です。
- サンプル数: 何枚のデータフレームを発生させるかです。
これらのパラメータを考慮してデータ発生のためのRのコードを書いていきます。
データ発生の関数定義
本章では、データ発生のコードについて記します。
一点注意事項ですが、以降のコードでは、mvtnormパッケージとtidyverseパッケージを使用します。これらパッケージをインストールされていない方は、まず下記のコードを実行してください。
install.packages("tidyverse")
install.packages("mvtnorm")
データ発生のコードは、下記のようになります。
(大変申し訳ないのですが、Rのシンタックスハイライトが上手く設定できず、色が微妙になっております)
Generate.2class.Data <- function(d, cs, m, s, r){
# 各引数について
# d: dimensionの略、変数次元
# cs: class sizeの略、クラス別サンプルサイズ
# m: muの略、平均ベクトルの要素
# s: sigmaの略、分散の大きさ
# r: rhoの略、相関の大きさ
# 多変量正規分布のパラメータ
mu1 <- rep(m[1], d) # クラス1の母平均ベクトル [d次元]
mu2 <- rep(m[2], d) # クラス2の母平均ベクトル [d次元]
Sigma1 <- matrix(r[1]*s[1], d, d) # クラス1の母共分散行列 [d x d]
Sigma2 <- matrix(r[2]*s[2], d, d) # クラス2の母共分散行列 [d x d]
diag(Sigma1) <- s[1] # 対角成分に値を代入 [d x d]
diag(Sigma2) <- s[2] # 対角成分に値を代入 [d x d]
# 説明変数行列 [n x d]
X <- rbind(rmvnorm(cs[1], mu1, Sigma1), # クラス1の説明変数
rmvnorm(cs[2], mu2, Sigma2)) %>% # クラス2の説明変数
as.data.frame() %>% # dataframeに変形
set_names(paste0("X", 1:d)) # 列名を作成
# クラスベクトル [n次元]
y <- c(paste0("C", rep(1, cs[1])), # C1,C1,...,C1 [n1次元]
paste0("C", rep(2, cs[2]))) # C2,C2,...,C2 [n2次元]
# 人工データ [n x (d+1)]
res <- X %>%
mutate(Target = y) # Xにクラスベクトルを追加
return(res) # 出力
}
上記のコードでは、Generate.2class.Dataという関数を定義しております。コードの意味は、コメントアウトで示した通りです。
データの発生
データの発生についてです。上記で定義したGenerate.2class.Data関数を実際に実行し、データの発生を行います。後々可視化することを考慮に入れ、今回は変数を2次元にいたします。
library(tidyverse)
library(mvtnorm)
set.seed(123) # seedの設定
size <- 100 # サンプルサイズ
c_ratio <- 0.5 # クラスの比率
c_size <- c(round(c_ratio * size),
size - round(c_ratio * size)) # クラス別サンプルサイズ
X_dim <- 2 # 変数次元
mu <- c(1, -1) # 平均
sig <- c(1, 1) # 分散
rho <- c(0, 0) # 相関
n_df <- 10 # サンプル数
# データの作成
dfs <- lapply(1:n_df, function(i) Generate.2class.Data(X_dim, c_size, mu, sig, rho))
上記コードを実行することで、データを発生できます。今回は2クラスのデータに絞っているため、c_size, mu, sig, rhoには2つの要素が含まれています。データはn_df個発生しており、dfsに格納されています。dfsはリスト型になっており、lapplyを用いてデータを格納しております(Pythonの内包表記をRでやっているようなイメージです)。dfsは下記のようにして実行する事も可能です。
dfs <- list()
for(i in 1:n_df){
dfs[[i]] <- Generate.2class.Data(X_dim, c_size, mu, sig, rho)
}
データの確認
データの発生はできたので、データの中身を簡単に確認しておきます。下記で実行しているコードは、「PythonのpandasとRのdplyr・tidyverseに関するデータフレーム操作コード比較」で説明をしているので、良かったら参考にしてください。
dfs[[1]] %>% head()
# X1 X2 Target
# 0.4395244 0.7698225 C1
# 2.5587083 1.0705084 C1
# 1.1292877 2.7150650 C1
# 1.4609162 -0.2650612 C1
# 0.3131471 0.5543380 C1
# 2.2240818 1.3598138 C1
dfs[[1]] %>% tail()
# X1 X2 Target
# -0.2459462 -1.4992920 C2
# -0.7855547 -1.3246859 C2
# -0.9054165 -1.8953634 C2
# -2.3108015 0.9972134 C2
# -0.3992912 -2.2512714 C2
# -1.6111659 -2.1854801 C2
dfs[[1]] %>% str()
# 'data.frame': 100 obs. of 3 variables:
# $ X1 : num 0.44 2.559 1.129 1.461 0.313 ...
# $ X2 : num 0.77 1.071 2.715 -0.265 0.554 ...
# $ Target: chr "C1" "C1" "C1" "C1" ...
dfs[[1]] %>% summary()
# X1 X2 Target
# Min. :-3.053247 Min. :-2.66794 Length:100
# 1st Qu.:-1.055414 1st Qu.:-1.28759 Class :character
# Median : 0.014842 Median :-0.10206 Mode :character
# Mean : 0.005807 Mean :-0.02295
# 3rd Qu.: 1.125213 3rd Qu.: 1.08055
# Max. : 3.187333 Max. : 3.16896
head()とtail()の箇所より、前半部分がクラス1、後半部分がクラス2のデータとなっていることが確認できます。また、str()の部分より、行数列数や各カラムの型もわかります。最後に、summary()の実行結果より、X_1, X_2の平均値が0付近になっていることが示されております。
可視化
上記では、データ簡単な確認を致しました。ここでは、実際に可視化して、どのような分布になっているか確認をします。下記のコードによってデータの散布図を描いてみます。
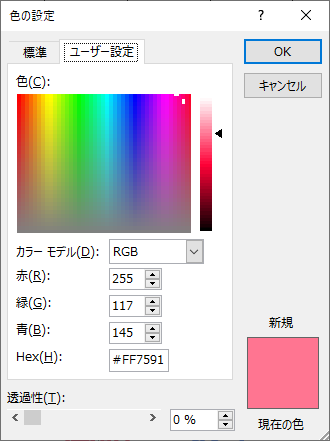
コード内でadd_rowを用いている理由は、データの中心を可視化するためです。今回は、(1,1)と(-1,-1)に丸に十字をプロットしています。また、themeを細かく設定しておりますが、「【背景色・文字色】ggplotのthemeで色違いのグラフ作成」でもthemeの説明をしているので、良かったら参考にしてみてください。加えて、グラフの色は"#FF7591", "#70A0FF"のようにHexで設定しています。このように色を指定することで、パワーポイントに貼り付けをした際に、統一感を出すことができます。Hexはパワーポイント色の設定から取得できます。
Rのコードを下記に示します。
lim <- 4 # グラフの表示範囲を指定
plot_scatter <- dfs[[1]] %>% # data.frameを指定
mutate(Target = str_replace(Target, pattern = "C", replacement = "Class")) %>% # CをClassに置換
add_row(X1 = c(mu[1],mu[2]), X2 = c(mu[1],mu[2]), Target = c("Center","Center")) %>% # データを2行追加
ggplot(aes(y = X2, x = X1, color = Target, shape = Target, size = Target)) + #通常のggplot
geom_hline(yintercept = 0, size = 0.2) + # x軸を引く
geom_vline(xintercept = 0, size = 0.2) + # y軸を引く
geom_point() + # 散布図
scale_color_manual(values = c("black","#FF7591","#70A0FF")) + # プロットの色を設定
scale_size_manual(values = c(6,3.5,3.5)) + # プロットの大きさを指定
scale_shape_manual(values = c(10,16,17)) + # プロットの形状を指定
scale_x_continuous(breaks = -lim:lim, limits = c(-lim, lim)) + # Xの範囲を指定
scale_y_continuous(breaks = -lim:lim, limits = c(-lim, lim)) + # Yの範囲を指定
theme_bw() + # themeを設定
theme(line = element_line(colour = "black", size = 0.5), # 線
rect = element_rect(colour = "black", fill = "white", size = 0.5), # 矩形
text = element_text(colour = "black", size = 15), # 文字
aspect.ratio = 1, # グラフの縦横比
plot.background = element_rect(fill = "white"), # グラフ外の色
panel.border = element_rect(colour = "black"), # グラフの枠線
panel.background = element_rect(colour = "black", fill = "white"), # グラフの背景色
panel.grid.major = element_line(size = 0.3, colour = "grey80"), # グラフのメイングリッド
panel.grid.minor = element_blank(), # グラフのマイナーグリッド:なし
axis.title = element_text(size = 13), # 縦横軸の名称
axis.ticks = element_line(size = 0.3), # 縦横軸の針
axis.text = element_text(colour = "black"), # 縦横軸の数字
legend.title = element_blank(), # 凡例のタイトル:なし
legend.text = element_text(size = 15), # 凡例の文字
legend.background = element_rect(colour = "black", size = 0.5), # 凡例の背景
legend.position = c(1,0), # 凡例の場所
legend.justification = c(1,0)) # 凡例の場所
plot_scatter # 表示
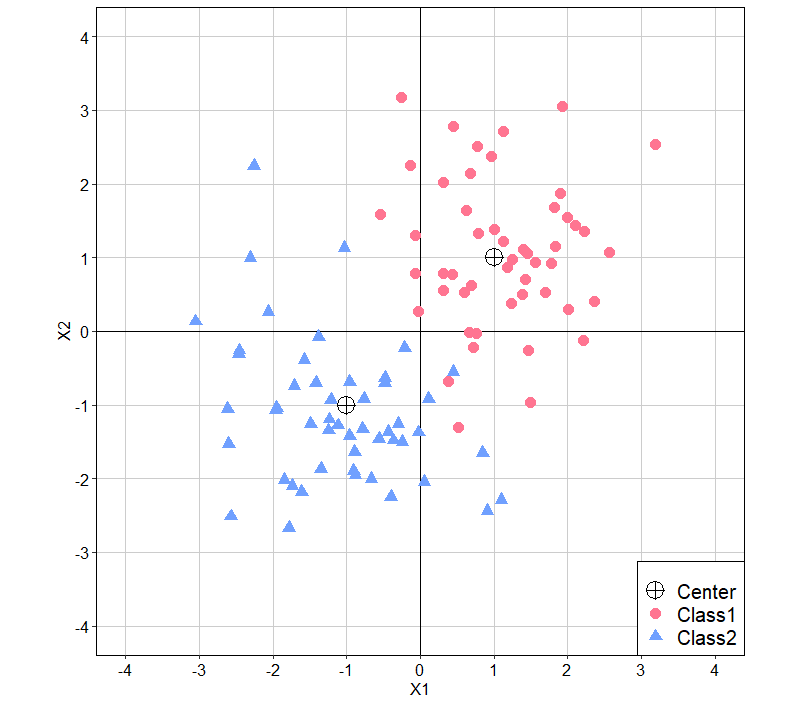
グラフを見ると、無相関・等分散・均衡のデータとなっていることがわかります。
別パターンのデータを確認
上記の設定では、単純なデータだったため、相関の発生や等分散性を崩した不均衡データの確認をします。
c_ratio: 0.5を0.9に変更。不均衡データになります。mu: (1, -1)を(2, -1)に変更。中心をずらすことができます。sig: (1, 1)を(1/3, 3)に変更。不均一分散データになります。rho: (0, 0)を(0.95, -0.6)に変更。相関のあるデータになります。
library(tidyverse)
library(mvtnorm)
set.seed(123) # seedの設定
size <- 100 # サンプルサイズ
c_ratio <- 0.9 # クラスの比率
c_size <- c(round(c_ratio * size),
size - round(c_ratio * size)) # クラス別サンプルサイズ
X_dim <- 2 # 変数次元
mu <- c(2, -1) # 平均
sig <- c(1/3, 3) # 分散
rho <- c(0.95, -0.6) # 相関
n_df <- 10 # サンプル数
# データの作成
dfs <- lapply(1:n_df, function(i) Generate.2class.Data(X_dim, c_size, mu, sig, rho))
そして先ほど同様可視化を行うと、下記のようになります。
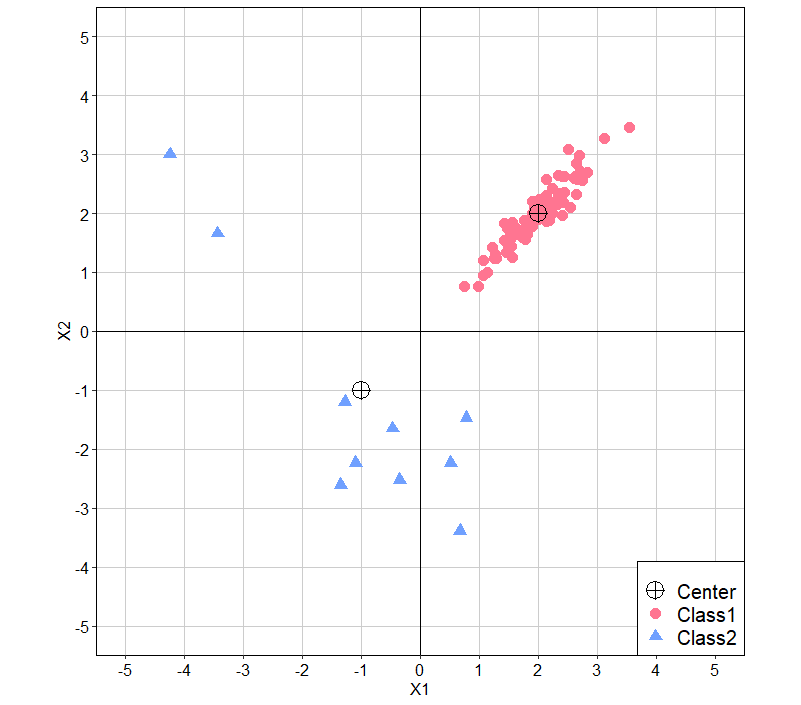
グラフを見ると、母数の変化が生成されるデータに反映されていることがわかります。
まとめ
以上で、『多変量正規分布によるクラス分類の人工データ発生と可視化』の記事を終わります。mvtnormを用いたデータ発生に関する日本語の解説は少ないので、少しでも参考になったら幸いです。
他にもRに関する記事は多くあるので、良かったら参考にしてください。

