概要
この記事では, 「効果検証入門」のポイントをまとめ, 書籍内で行われている分析を掲載していきます.
(本記事は自分が勉強したことのまとめ的要素が強いので, 手元に書籍がある状態でお読みいただくことをオススメします)
尚, 分析コードについては著者が提供しているGitHubからダウンロードもできますので, 実際に手を動かしてみたい方は参考にしてください.
今回は第2章 回帰分析の後半について取扱います.(P67~P90が該当)
ここでは実際の論文データを元に回帰分析の演習を行います.
また, 過去のブログについては以下をご参照ください.
2.3 回帰分析を利用した探索的な効果検証(P67~P83)
PACESによる学費の割引券配布の概要
-
コロンビアで行われた教育に関する実証実験をここでは扱う
-
ランダムに学費割引券を配ることで, (コロンビアでは)より良い教育を受けるための効果的な手段である私立高校に通いやすくする(ただし途中で留年したら剥奪)
- 教育の質向上, 留年の減少が期待される
- この介入から数年後に割引券に当選した人, しなかった人それぞれに電話インタビューを行うことでデータを取得
- 一見するとRCTが実現されていそうだが, 落選して公立にしか通えず所得が低いので回答したくない, などの傾向が発生する可能性もある
-
ランダムに学費割引券を配ることで, (コロンビアでは)より良い教育を受けるための効果的な手段である私立高校に通いやすくする(ただし途中で留年したら剥奪)
Rによる回帰分析の実行
- 割引券がどのような影響を与えているか調べる
# 使用するデータのダウンロード
devtools::install_github("itamarcaspi/experimentdatar")# パッケージの読み込み
library(tidyverse)
library(ggplot2)
library(broom)
library(experimentdatar)# データの読み込み
data(vouchers)## 割引券をもらったかどうか
formula_x_base <- "VOUCH0"
# 共変量の設定
formula_x_covariate <- "SVY + HSVISIT + AGE + STRATA1 + STRATA2 + STRATA3 + STRATA4 + STRATA5 + STRATA6 + STRATAMS + D1993 + D1995 + D1997 + DMONTH1 + DMONTH2 + DMONTH3 + DMONTH4 + DMONTH5 + DMONTH6 + DMONTH7 + DMONTH8 + DMONTH9 + DMONTH10 + DMONTH11 + DMONTH12 + SEX2"
# 目的変数の設定
formula_y <- c("TOTSCYRS","INSCHL","PRSCH_C","USNGSCH","PRSCHA_1","FINISH6","FINISH7","FINISH8","REPT6","REPT","NREPT", "MARRIED","HASCHILD","HOURSUM","WORKING3")
# yに対しての共変量を含まない回帰式
## 回帰式の文字列を作成
base_reg_formula <- paste(formula_y, "~", formula_x_base)
## それぞれの回帰式名に"_base"を付与
names(base_reg_formula) <- paste(formula_y, "base", sep = "_")
# 共変量を含んだ回帰式
## 回帰式の文字列を作成
covariate_reg_formula <- paste(formula_y, "~", formula_x_base, "+", formula_x_covariate)
## それぞれの回帰式名に"_covariate"を付与
names(covariate_reg_formula) <- paste(formula_y, "covariate", sep = "_")
# それぞれの回帰式名の列を結合
table3_formula <- c(base_reg_formula, covariate_reg_formula)
# データフレーム化
models <- table3_formula %>%
enframe(name = "model_index", value = "formula")
# 回帰分析を実行する
## bogota1995のデータを抽出する
regression_data <- vouchers %>%
filter(TAB3SMPL == 1, BOG95SMP == 1)
## まとめて回帰分析を実行
df_models <- models %>%
mutate(model = map(.x = formula, .f = lm, data = regression_data)) %>%
mutate(lm_result = map(.x = model, .f = tidy))
df_results <- df_models %>%
## 文字列に直す
mutate(formula = as.character(formula)) %>%
## 抽出する列を選択
## ここまでだとlm_resultがネスト状態になっている
select(model_index, formula, lm_result) %>%
## lm_rsultをunnestする
unnest(cols = c(lm_result))私立学校への通学と割引券の利用についての分析
-
まずは割引券が適切に使われているかを確認する
- PRSCHA_1は6年生スタート時に私立学校に在籍していたか
- USNGSCHは調査期間中に何らかの奨学金を使ったか
# 通学率と奨学金の利用
using_voucher_results <- df_results %>%
## 割引券の利用効果を抜き出す
## str_detectでいずれかの文字を含む行を選択している(|がorを意味している)
filter(term == "VOUCH0", str_detect(model_index, "PRSCHA_1|USNGSCH")) %>%
select(model_index, term, estimate, std.error, p.value) %>%
## データを昇順に並び替え
arrange(model_index)#取り出した効果の可視化
using_voucher_results %>%
ggplot(aes(x = model_index, y = estimate)) +
geom_point() +
## 95%信頼区間の設定
geom_errorbar(aes(ymax = estimate + std.error*1.96,
ymin = estimate - std.error*1.96,
width = 0.1)) +
theme(axis.text.x = element_text(angle = 45, hjust = 1),
plot.title = element_text(hjust = 0.5),
legend.position = "bottom",
plot.margin = margin(0.5,1,0.5,1, "cm"))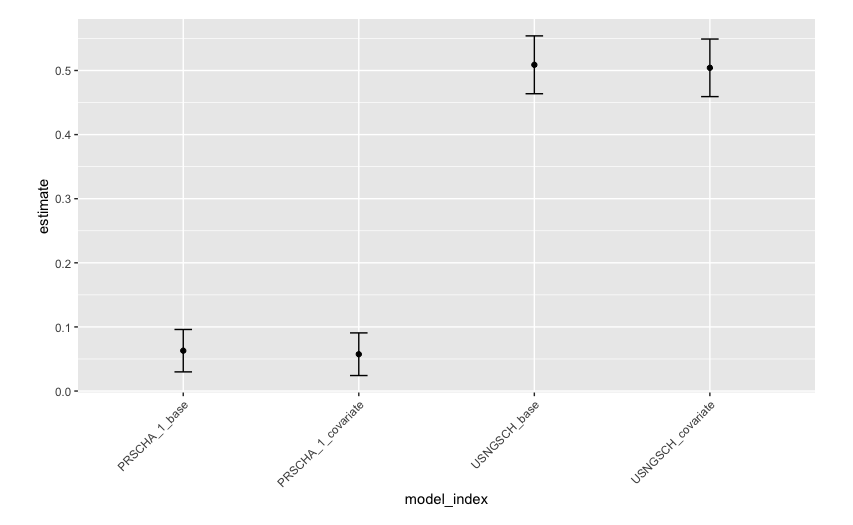
- 結果の解釈
- PRSCHA_1の結果は当選グループのほうが私立学校に在籍している割合が6%程度増加していることを示唆している
- USNGSCHの結果は当選グループのほうが50%程度多く, 非当選グループより奨学金を利用していることを示す
- 割引券自体は使われているものの, 元々の私立進学率が高いので効果が限定的になってる
割引率は留年を減らしているのか?
- 本制度では留年をすると割引が消滅してしまうので, 勉強に対するモチベーションが増加すると予想できる. そこで, 留年に関する変数が割引券によってどう変化しているかを検証する
# 留年の傾向を可視化
## 進学や留年に関する変数を抜き出す
going_private_results <- df_results %>%
filter(term == "VOUCH0",
str_detect(model_index, "PRSCH_C|INSCHL|FINISH|REPT")) %>%
select(model_index, term, estimate, std.error, p.value) %>%
arrange(model_index)
going_private_results %>%
#共変量を追加しているものだけ抜き出す
filter(str_detect(model_index, "covariate")) %>%
ggplot(aes(x = model_index, y = estimate)) +
geom_point() +
geom_errorbar(aes(ymax = estimate + std.error*1.96,
ymin = estimate - std.error*1.96,
width = 0.1)) +
## y=0に線を引く
geom_hline(yintercept = 0, linetype = 2) +
## 軸の設定
theme(axis.text.x = element_text(angle = 45, hjust = 1),
plot.title = element_text(hjust = 0.5),
legend.position = "bottom",
plot.margin = margin(0.5,1,0.5,1, "cm"))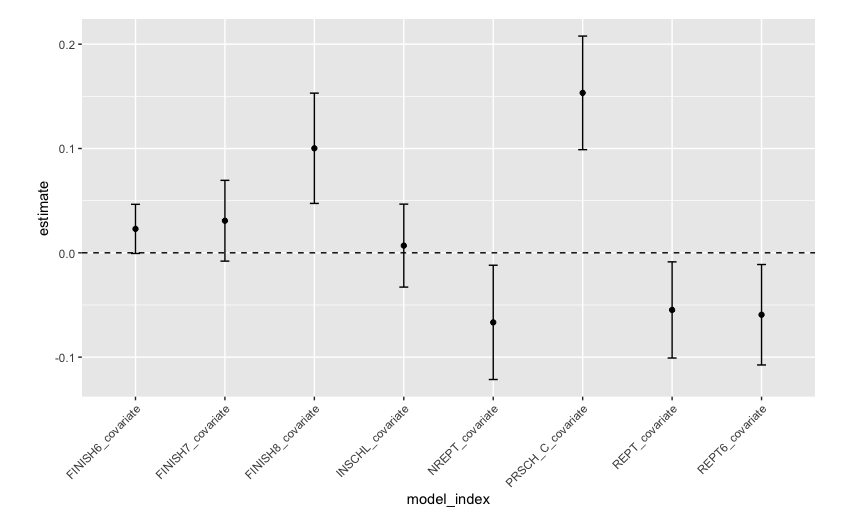
-
結果の解釈
-
PRSCHは当選から3年後に私立学校に通っていたか
- 当選していると通い続ける生徒が約15%増加したとわかる
-
INSCHLは公立私立問わず通学の傾向を示す
- 信頼区間が0を跨いでいるので, 効果は確認できないため, 学校に通える生徒の増加は期待できない
-
REPT6は6年生で留年したかどうか
- 当選していると6%程度減少しているとわかる
- FINISH8は3年間で8年生を修了したかなので, 10%程度割引券の効果が効いていることが確認できる
-
PRSCHは当選から3年後に私立学校に通っていたか
- ここまでで私立学校への進学を維持し, かつ留年を防止できていそうなことはわかった. しかし, 私立学校の教育の質が高いから留年しなくなったということも考えられる. 今回のデータではそこまでは言及できない
性別による効果差
- 割引券の効果が性別によって異なるのかを検証する
# 論文内のteble4を作成する
## 使用するデータの抽出
data_tbl4_bog95 <- vouchers %>%
filter(BOG95SMP == 1, TAB3SMPL == 1,
!is.na(SCYFNSH), !is.na(FINISH6), !is.na(PRSCHA_1),
!is.na(REPT6), !is.na(NREPT), !is.na(INSCHL),
!is.na(FINISH7),!is.na(PRSCH_C), !is.na(FINISH8),
!is.na(PRSCHA_2), !is.na(TOTSCYRS), !is.na(REPT)) %>%
select(VOUCH0, SVY, HSVISIT, DJAMUNDI, PHONE, AGE,
STRATA1:STRATA6, STRATAMS, DBOGOTA, D1993, D1995, D1997,
DMONTH1:DMONTH12, SEX_MISS, FINISH6, FINISH7, FINISH8,
REPT6, REPT, NREPT, SEX2, TOTSCYRS, MARRIED, HASCHILD,
HOURSUM,WORKING3, INSCHL,PRSCH_C,USNGSCH,PRSCHA_1)## 女子生徒のデータを抜き出す(SEX2=0が女性)
regression_data_female <- data_tbl4_bog95 %>% filter(SEX2 == 0)## 回帰分析の実行
df_models_female <- models %>%
mutate(model = map(.x = formula, .f = lm, data = regression_data_female)) %>%
mutate(lm_result = map(.x = model, .f = tidy))## データの整形
df_results_female <- df_models_female %>%
### gender列を追加
mutate(formula = as.character(formula), gender = "female") %>%
select(formula, model_index, lm_result, gender) %>%
unnest(cols = c(lm_result))## 男子生徒のデータを抜き出す
regression_data_male <- data_tbl4_bog95 %>% filter(SEX2 == 1)## 回帰分析の実行
df_models_male <- models %>%
mutate(model = map(.x = formula, .f = lm, data = regression_data_male)) %>%
mutate(lm_result = map(.x = model, .f = tidy))## データの整形
df_results_male <- df_models_male %>%
### gender列を追加
mutate(formula = as.character(formula), gender = "male") %>%
select(formula, model_index, lm_result, gender) %>%
unnest(cols = c(lm_result))## 私立に通う傾向PRSCHA_1と, 奨学金を使う割合USNGSCHに関する分析結果を抜き出す
### 行方向で結合
using_voucher_results_gender <- bind_rows(df_results_male, df_results_female) %>%
filter(term == "VOUCH0", str_detect(model_index, "PRSCHA_1|USNGSCH")) %>%
select(gender, model_index, term, estimate, std.error, p.value) %>%
### 並び替え
arrange(gender, model_index) %>%
filter(str_detect(model_index, "covariate"))##結果の可視化
using_voucher_results_gender %>%
ggplot(aes(y = estimate, x = model_index)) +
geom_point(aes(colour = gender)) +
### 信頼区間
geom_errorbar(aes(ymax = estimate + std.error*1.96,
ymin = estimate - std.error*1.96,
width = 0.1,
colour = gender)) +
### y = 0の直線を描く
geom_hline(yintercept = 0, linetype = 2) +
theme(axis.text.x = element_text(angle = 45, hjust = 1),
plot.title = element_text(hjust = 0.5),
### x軸のタイトルの位置
legend.position = "bottom",
plot.margin = margin(0.5,1,0.5,1, "cm")) +
### 指定した行と列で分割(ここではgenderで行方向に分割している)
facet_grid(gender ~ .)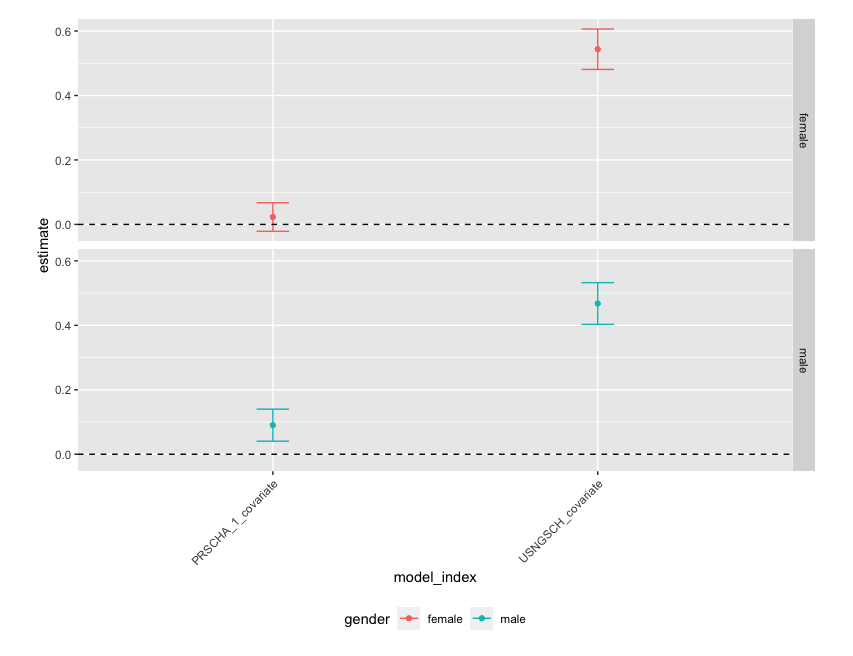
-
結果の解釈
- 男性は当選すると10%程度私立に行く傾向が強くなるが, 女性は効果なしという可能性を否定できない(統計的に有意ではない)
- 一方奨学金の利用については男性が45%程度, 女性が55%程度の効果が示唆されており, 女性のほうが当選した場合奨学金を使う可能性が高いことが考えられる
- 次に, 進学し続ける効果があるのかを確認する
## 留年と通学年数
going_private_results_gender <- bind_rows(df_results_male, df_results_female) %>%
### 使うデータの抽出
filter(term == "VOUCH0",
str_detect(model_index, "PRSCH_C|INSCHL|REPT|TOTSCYRS|FINISH")) %>%
select(gender, model_index, term, estimate, std.error, p.value) %>%
arrange(model_index)going_private_results_gender %>%
filter(str_detect(model_index, "covariate")) %>%
ggplot(aes(x = model_index, y = estimate))+
geom_point(aes(colour = gender))+
geom_errorbar(aes(ymax = estimate + std.error*1.96,
ymin = estimate - std.error*1.96,
width = 0.1,
colour = gender)) +
geom_hline(yintercept = 0, linetype = 2) +
theme(axis.text.x = element_text(angle = 45, hjust = 1),
plot.title = element_text(hjust = 0.5),
### x軸のタイトルの位置
legend.position = "bottom",
plot.margin = margin(0.5,1,0.5,1, "cm")) +
facet_grid(gender ~ .)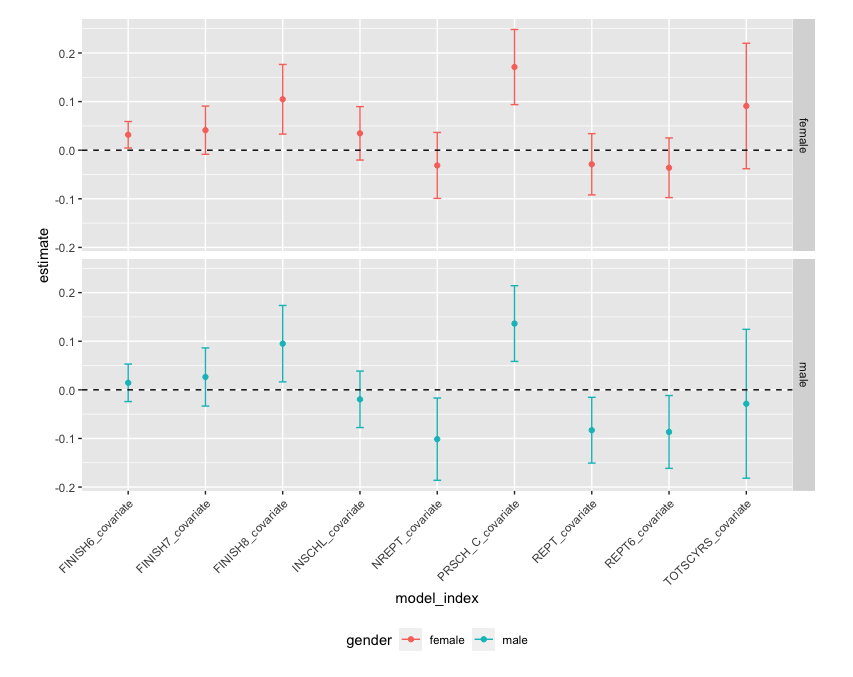
-
結果の解釈
- 私立学校への通学継続を表すPRSCH_Cは男性13%程度, 女性17%程度プラスの効果があると考えられる
- より高い学年を修了できるか(FINISH6~8)は男女ともそれほど結果に変わりはなく, 8年生の修了は10%程度増加している
-
ただし留年に関するNREPTやREPTに関しては女子の結果は有意ではなく, 全体の結果とは異なり女子に対して留年に対する効果はほぼない
- これは家庭内の経済的影響等を女性のほうが受けやすいのではといった原因が想像できる
- 最後に男女別に労働時間を確認する
working_hour_results_gender<- bind_rows(df_results_male, df_results_female) %>%
filter(term == "VOUCH0", str_detect(model_index, "HOUR") ) %>%
select(gender, model_index, term, estimate, std.error, p.value) %>%
arrange(model_index)working_hour_results_gender %>%
filter(str_detect(model_index, "covariate")) %>%
ggplot(aes(x = model_index, y = estimate))+
geom_point(aes(colour = gender))+
geom_errorbar(aes(ymax = estimate + std.error*1.96,
ymin = estimate - std.error*1.96,
width = 0.1,
colour = gender)) +
geom_hline(yintercept = 0, linetype = 2) +
theme(axis.text.x = element_text(angle = 45, hjust = 1),
plot.title = element_text(hjust = 0.5),
legend.position = "bottom",
plot.margin = margin(0.5,1,0.5,1, "cm")) +
### 列方向に分割
facet_grid(. ~ gender)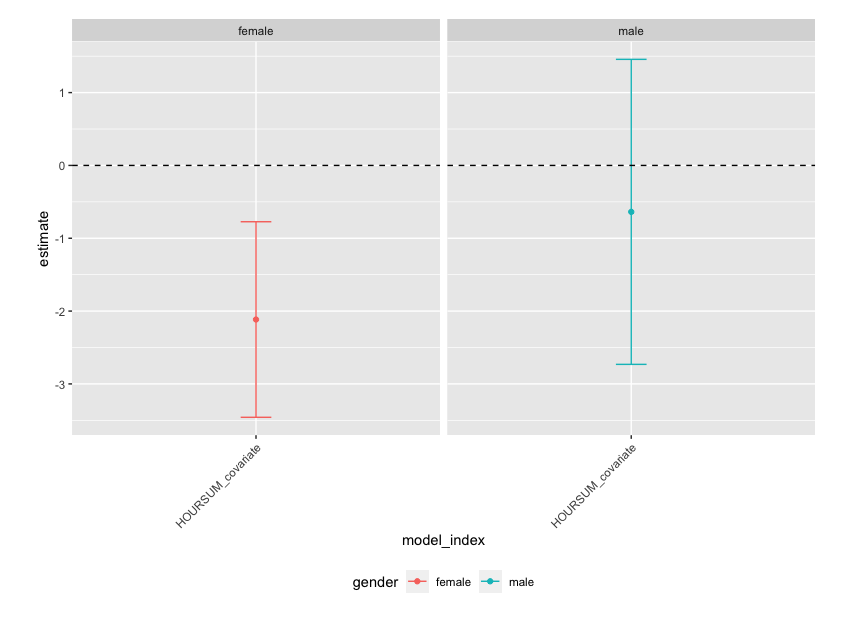
-
結果の解釈
- 女性においては労働時間の減少が統計的に有意な結果として確認される
2.4 回帰分析に関するさまざまな議論(P83~P90)
予測と効果推定
- 予測を目的にしている場合は予測能力の高さが求められるが, 効果検証の文脈においては有用であるという保証はないので考慮しない
制限被説明変数(Limited Dependent Variable)
-
目的変数の分布に関しては取りうる値によって適したモデルを選択する必要がある
-
例えば, ある商品を買ったか否かのように0か1の値しか取らないものはロジスティック回帰を選択する
- このように目的変数が特定の値しかとらないような制約がある状態を制限被説明変数という
- 本書では介入変数Zが0か1の離散値を取るため, E[Y|Z=1]とE[Y|Z=0]の関係は線形になるので線形回帰で分析を実行している
-
例えば, ある商品を買ったか否かのように0か1の値しか取らないものはロジスティック回帰を選択する
対数を利用した回帰分析
- 目的変数Yに対してlogをとるとYに何%の影響があったかを確認できる
-
変数Xの対数をとった場合, Xを1%変化させた時にYにどの程度影響を与えるか確認できる
- 例えばある変数Xに対する係数が0.1だった場合, Xが1単位増加すると目的変数が10%高くなる
多重共線性
-
1つのモデルから複数の変数に関する情報を得ることを想定して回帰分析を実行する場合, 変数同士の強い相関(多重共線性)が発生する可能性がある
- 変数間の相関が強い場合, 推定値の分散が大きくなり標準誤差が信頼できないものとなってしまう
- ただし, 介入の変数以外で多重共線性がある場合は興味のあるパラメータには影響はない(介入変数で発生している場合は十分に配慮する必要がある)
パラメータの計算
-
重回帰分析における介入の効果は, 以下のように算出される.
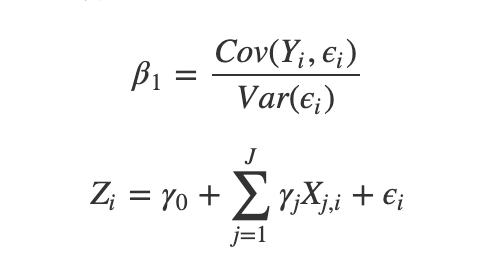
- ここで\epsiloniは,Ziに対してほかの共変量X_{i,j}を回帰させたときの残差である
- この残差とYの共分散を残差の分散で割ったものが推定値となる
- また, 共変量が0,1の値しかとらない場合は共分散は共変量の値がXの時の平均の差を介入変数の分散で重みつけしたものになるので, 介入変数の分散が大きいXの値を持つデータは, パラメータの推定結果を大きく左右する. 式にすると以下のようになる \beta_1 = \frac{E[Var(Z|X)(E[Y|Z=1, X] - E[Y|Z = 0, X])]}{E[Var(Z|X)]}
-
ここでE[Var(Z|X)=P(Z=1|X)(1-P(Z=1|X)となるので,P(Z=1|X)=0.5の時最大になる
-
よって, 介入と非介入のグループが50:50だと結果に最も大きく影響を与えることになる
RCTの場合は介入グループと非介入グループの割合の期待値はどのXにおいても0.5となるので, 回帰分析はデータの平均的効果(ATE)を推定していることになる
おわりに
今回のように少し複雑なデータでは分析の背景や事前知識をしっかり抑えておかないと効果的な分析は難しいなと感じました.そう考えると, 有益な分析ができるかどうかは調査設計の段階から決まってくることを痛感させられます.
第3章では傾向スコアを用いた分析を扱っていきます.
最後までお読みいただきありがとうございました.