PyStanでベイズ推論+MCMC法によるデータ分析③(単回帰モデル)
はじめに
こんにちはdeepblueでインターン生として働いている東です。
この記事は連載3記事目です。まだ読んでいない方は読んでいただけると嬉しいです。
まだまだ分析入門者ですが頑張ります。
PyStanでベイズ推論+MCMC法によるデータ分析②(MCMCの結果と評価)
前回の記事と今回の概要
前回前々回ではPyStanで乱数を発生させてその評価を行いました。本記事で単回帰モデルを使用して売り上げデータの予測を行います。
今回はRとStanではじめるベイズ統計モデリングによるデータ分析入門第3部以降を参考にしています。
こちらが参考図書です。
使用データ
今回使用するビールの売り上げと気温データはこちらのデータです。
モジュール、データの読み込みと散布図のプロットをしています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# pystanの読み込み
import pystan
# seabornライクのデザインに設定
import seaborn as sns; sns.set()
# データの読み込み
df = pd.read_csv(path+'3-2-1-beer-sales-2.csv')
# 散布図の可視化
plt.figure(figsize=(14,7))
plt.scatter(df.temperature, df.sales, color='black')
plt.xlabel('temperature', fontsize=18)
plt.ylabel('sales', fontsize=18)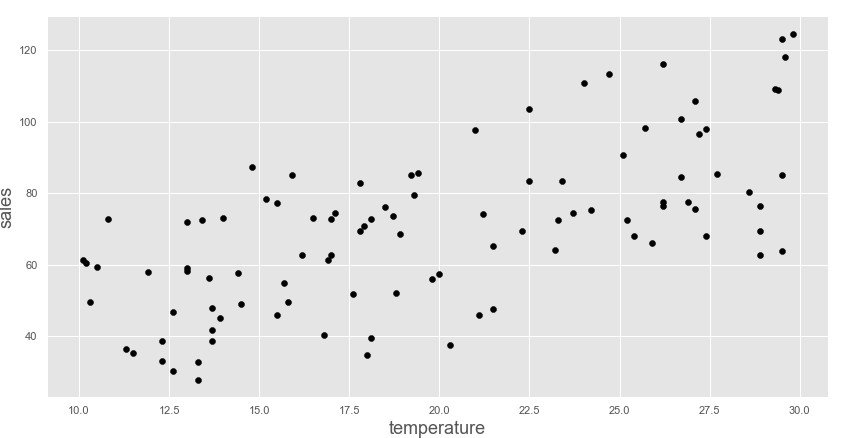
散布図を描いてみたところtemperatureとsalesのデータには正の相関がありそうなので単回帰モデルで売り上げ予測をしてみます。点の色やグラフスタイルは自分好みに変更してあります。
モデル構造とStanファイル
stanファイルはこちらからダウンロードしました。
今回の統計モデルは下のように設定します。気温temperatureから売り上げsalesを単回帰モデルで推定します。回帰におけるinterceptは切片、\betaが係数に当たり売り上げsalesは正規分布に従うとします。
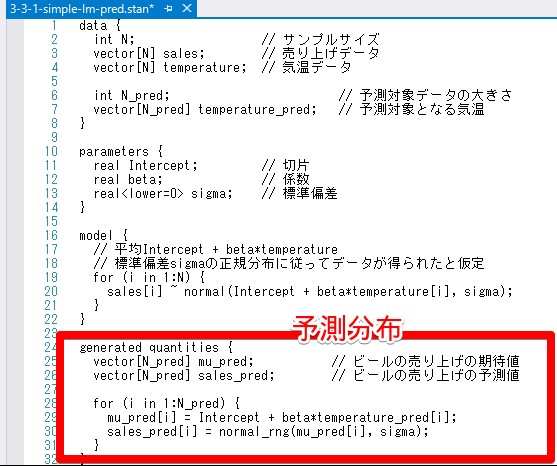
generated quantities{...}
乱数を生成することできるブロックで事後分布に従う予測はここで行う。
実行している順序が難しいですしコードを書くときもこの順番でなければならないようです。
PyStanの実行結果
PyStanで実行してみます。散布図の気温の最小値と最大値から10度から30度で事後予測分布を生成します。
#ファイルの読み込み
df=pd.read_csv(path+'3-2-1-beer-sales-2.csv')
stan=path+'3-3-1-simple-lm-pred.stan'
temperature_pred=[i for i in range(10,31)]
#Stanに受け渡すために辞書形式に変形
data_list={'N':len(df),'sales':df.sales.values,'temperature':df.temperature.values,'N_pred':len(temperature_pred),'temperature_pred':temperature_pred}
#PyStanの実行
mcmc_result = pystan.stan(file=stan,data=data_list, iter=2000, chains=4, thin=1, warmup=1000 , seed=1)
print(mcmc_result)
#気温別の売り上げ平均の可視化
fig, axes = plt.subplots(nrows=2, ncols=1,figsize=(20,12))
for i in range(0,21):
string=str(i+10)+'Cº '
sns.distplot(mcmc_sample['mu_pred'][:,i]
,bins=14
,label=string+'_mu'
,hist=False
,ax=axes[0])
axes[0].set_title('mu',fontsize=30)
#気温別の売り上げの可視化
for i in range(0,21):
string=str(i+10)+'Cº '
sns.distplot(mcmc_sample['sales_pred'][:,i]
,bins=14
,label=string+'_sales'
,hist=False
,ax=axes[1])
axes[1].set_title('sales',fontsize=30)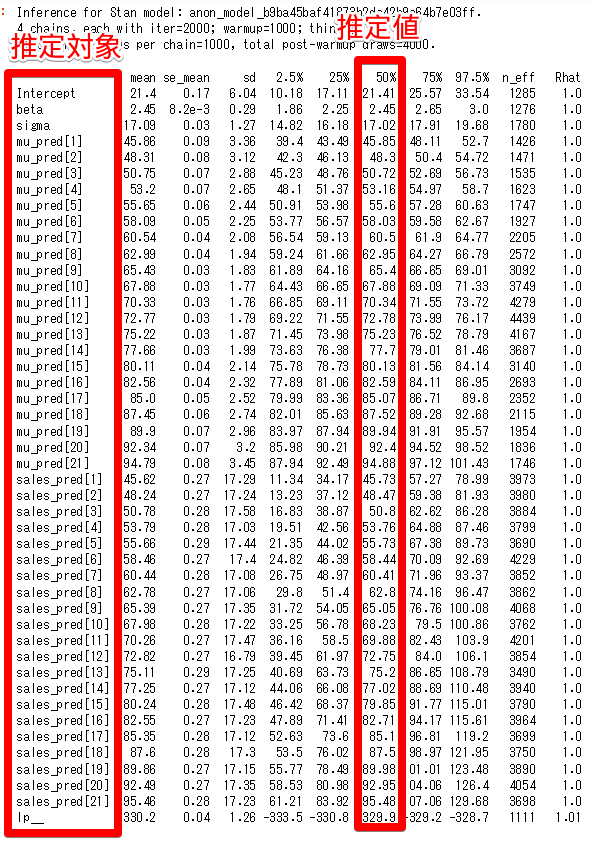

Rhatがほとんど1.0となっていることから収束が確認できます。事後分布に従う乱数を生成することができます。平均値の分布にばらつきがあるのは少し気になるところです。
予測分布の可視化
気温とその事後中央値から回帰直線を推定することができます。平均値に対する事後分布の2.5%区間から97.5%区間までを得ることができるので描いてみます。今回もコードは可視化がメインとなってしまいました。
回帰直線95%信用区間
#売り上げと気温の関係を散布図で確認
plt.scatter(df.temperature,df.sales, color='black')
plt.figure(figsize=(14,7))
plt.xlabel('temperature', fontsize=18)
plt.ylabel('sales', fontsize=18)
#95%信用区間の抽出
reg_95 = np.empty((0,2), float)
for x in range(21):
reg_95=np.append(reg_95,np.quantile(mcmc_sample['mu_pred'][:,x],q=[0.025,0.975]).reshape(1,2),axis=0)
#回帰直線のプロット
plt.plot([x for x in range(10,31)],[Intercept+x*beta for x in range(10,31)],color='blue')
#95%信用区間の描画
plt.fill_between([x for x in range(10,31)]
,reg_95[:,0]
,reg_95[:,1]
,color='blue',alpha=0.1)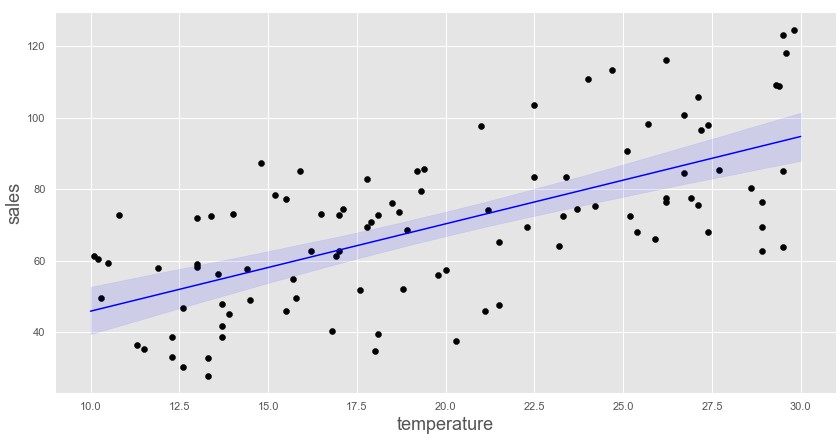
回帰直線の信用区間にばらつきがありますが、もっともらしい直線が引けている気がします。
売り上げ予想95%信用区間
#売り上げと気温の関係を散布図で確認
plt.scatter(df.temperature,df.sales,color='black')
plt.figure(figsize=(14,7))
plt.xlabel('temperature',fontsize=18)
plt.ylabel('sales',fontsize=18)
#95%信用区間の抽出
sales_95 = np.empty((0,2), float)
for x in range(21):
sales_95=np.append(sales_95,np.quantile(mcmc_sample['sales_pred'][:,x], q=[0.025,0.975]).reshape(1,2), axis=0)
#回帰直線のプロット
plt.plot([x for x in range(10,31)], sales_pred, color='blue')
#95%信用区間の描画
plt.fill_between([x for x in range(10,31)]
,sales_95[:,0]
,sales_95[:,1]
,color='blue',alpha=0.1)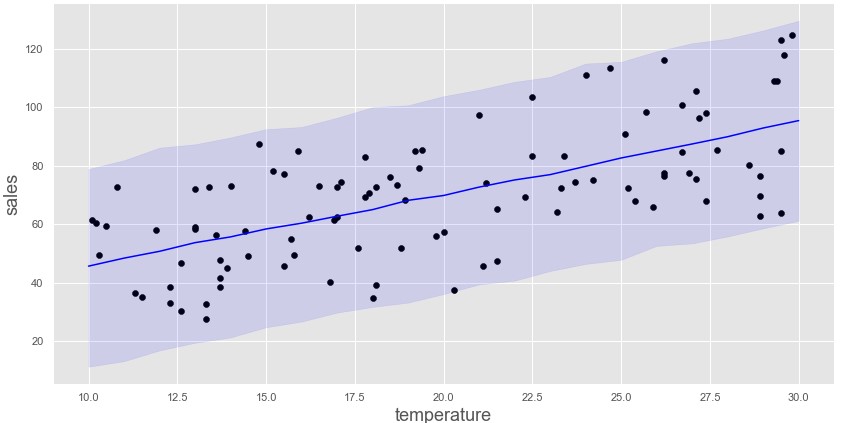
今回の例では予測区間からデータがはみ出ているデータ数からも推定したモデルの評価を行う際に有効かもしれません。
まとめ
いかがだったでしょうか?今回も可視化がメインになってしまいましたが、少しでもMCMCの理解が深まれば幸いです。次回以降はkaggleのデータセットなどを使って分析ができたらと思ってます。
良かったら見てください。