はじめに
ベイズ推論の枠組みで、事後分布の推論などに用いるマルコフ連鎖モンテカルロ法(通称:MCMC)の概要について、簡単に説明してみたいと思います。対象は、最初の「ベイズ推論におけるMCMCの必要性」を読んで、理解いただける方になると思います。
ベイズ推論におけるMCMCの必要性
データをX、パラメータ(潜在変数)を\thetaと書くこととします。確率モデル(尤度モデル)をp(X|\theta)、事前分布をp(\theta)とすると、事後分布は以下のように計算できます。
p(\theta|X) = \frac{p(X|\theta)p(\theta)}{p(X)}
ここで、重要となるのがp(X)の存在です。 p(\theta|X)が確率分布であるためには以下の条件が必要となります。
\int p(\theta|X) d\theta = \int \frac{p(X|\theta)p(\theta)}{p(X)}d\theta = 1
2つ目の等号について、両辺に p(X)をかけると
p(X) = \int p(X|\theta)p(\theta) d\theta
となります。要するに1番最初の式で、事後分布を解析的に求める場合、上の積分計算によってp(X)を求めなければなりません。しかし、一般にはこの積分計算は解析的に実行できません。そこで、登場するのが、MCMCです。
MCMCを端的に説明すると、「解析的に事後分布p(\theta|X)を計算せずとも、近似的に事後分布からサンプリングする方法」と言えます。事後分布からサンプリングできれば、以下のモンテカルロ法を用いて、平均・分散などの各種統計量を求めることができます。以降では、モンテカルロ法について説明した後に、「近似的な事後分布からサンプリング」を行う具体的な方法を説明していきます。
モンテカルロ法
モンテカルロ法は、乱数生成による数値計算手法です。ここでは、簡単な期待値計算の例について考えてみましょう。
確率分布~p(x)の期待値、すなわち確率変数~Xの厳密な平均値は以下の値で定義されます。
E[X]=\int xp(x)dx
定義から明らかなように、この値は積分計算によって求めますが、以下のように近似的に求めることもできます。
E[X]\approx \frac{1}{N}\sum_{i=1}^{N} x_i
ここで、x_iは~p(x)からの独立なサンプルです。右辺の値は、確率変数~Xの標本平均であることを考えると、期待値と近い値であることが期待されます。なお~N \rightarrow \infty において、大数の法則から標本平均は期待値に(確率)収束します。
このように、厳密な積分によってではなく、確率分布からの乱数(サンプリング)によって期待値計算を行う手法がモンテカルロ法と呼ばれる手法です。(本来はもっと広義です)
マルコフ連鎖
マルコフ連鎖とは、確率変数列 { X_t}_{t=0}^{\infty} に対して、以下で定義される概念です。
p(x_t|x_{t-1},x_{t-2},\dots)=p(x_t|x_{t-1})
要するに、t期における確率変数~X_tの条件付き分布が、一期前の確率変数~X_{t-1}の値にのみ依存するとき、確率変数列 { X_t}_{t=0}^{\infty} はマルコフ連鎖であると言います。
マルコフ連鎖である確率変数列{ X_t}_{t=0}^{\infty} の同時分布は、
\begin{aligned} p(x_0,\cdots,x_t) &=p(x_0)p(x_1|x_0)\times \cdots \times p(x_t|x_{t-1},\dots,x_0)\ &=p(x_0)\prod_{i=1}^t p(x_{i}|x_{i-1})\end{aligned}
と書き直すことができます。ここで、p(x_{i}|x_{i-1}) を遷移核と呼び、 K(x_{i-1},x_i) と書くこととします。
遷移核 K(x_{i-1},x_i) は、「 (i-1)期にx_{i-1}にいて、 i期にx_{i}に移動する確率」と解釈できます。すなわち、遷移核はマルコフ連鎖である確率変数列の移動ルールであると言えます。スタート地点である x_0と移動ルール K(x_{i-1},x_i) を決めてしまえば、確率変数列 { X_t}_{t=0}^{\infty} の挙動は完全に決定してしまいます。このことから、遷移核 K(x_{i-1},x_i) がマルコフ連鎖において極めて重要な要素であることがおわかりいただけると思います。
もう一度確認しておくと、上式に従う「確率変数列 { X_t}_{t=0}^{\infty} 」がマルコフ連鎖であり、その中でも移動ルールを記述している上式の「確率分布」が遷移核に対応しています。用語の定義を混同しないように気をつけてください。
マルコフ連鎖の具体例
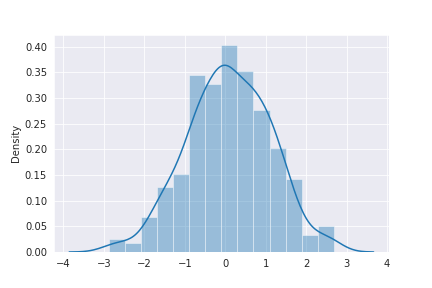
マルコフ連鎖の具体例として、ARモデルが挙げられます。最もシンプルなARモデルであるAR(1)モデルは、
p(x_i|x_{i-1})=\mathcal{N}(\rho x_{i-1},\sigma^2) と書くことができます。確率変数 X_iの条件付き分布が一期前の値 x_{i-1} にのみ依存しているので、この確率分布に従う確率変数列はマルコフ連鎖であり、このマルコフ連鎖の遷移核(移動ルール)は、上式そのものです。
下図は、 (\rho,\sigma^2)=(0.5,1)とした場合の確率変数列 { X_t}_{t=0}^{\infty} のサンプルをプロットしたものになります。
定常分布
MCMCを考える上で、重要な概念が定常分布です。定義から厳密に述べると少し難しいので、ここでは直感的な理解に留めたいと思います。
下図は、先ほどの図にサンプルした確率変数列のヒストグラムを添えたものです。
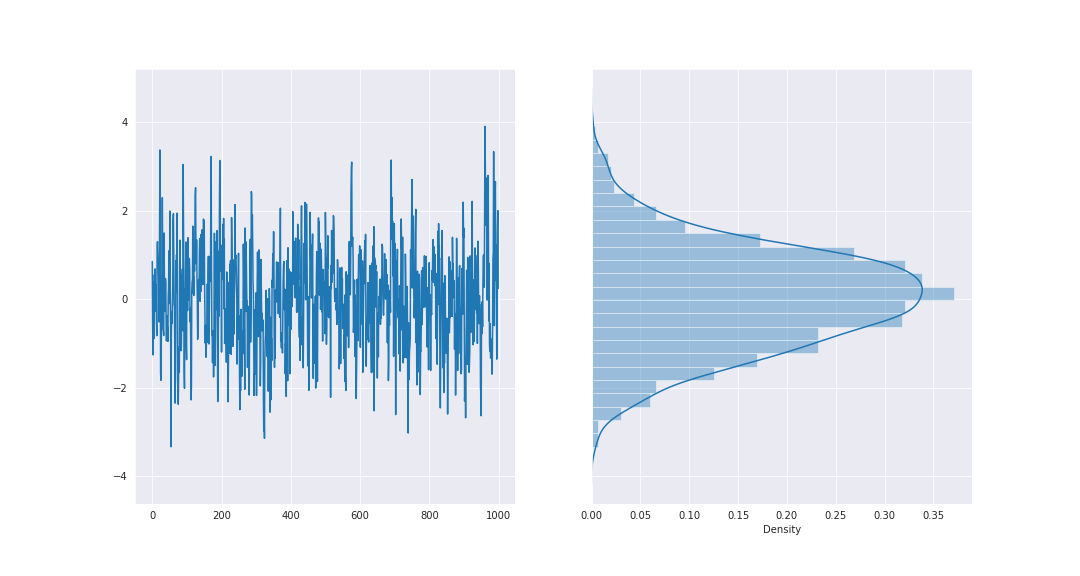
定常分布は、このヒストグラムに対応したような概念で、確率変数列を横から見たときに個々の確率変数X_iが従っている確率分布であると見なすことができます。もう少し丁寧に述べると、「定常分布Pを持つマルコフ連鎖に従う確率変数列{ X_t}_{t=0}^{\infty} の各要素である確率変数X_iは、定常分布Pに従う」と言えます。要するに、
X_t \sim P
のようなイメージで考えることができます。(厳密には少し異なるので、あくまでイメージとして認識してください)
事後分布の推論
最初に述べたように、MCMCを用いる目的は、「近似的に事後分布からサンプリングする」ことでした。ここで仮に、定常分布として事後分布を持つマルコフ連鎖があったとすると、このマルコフ連鎖の各要素X_tは定常分布である事後分布に従う確率変数であると見なすことができる、すなわちマルコフ連鎖の各要素を近似的に事後分布からのサンプルと見ることができるわけです。
ここまでの話をまとめると、定常分布として事後分布を持つマルコフ連鎖を構築できれば、マルコフ連鎖の各要素 X_tは事後分布からのサンプルとみなせるという話でした。また、マルコフ連鎖は遷移核によって定められるものであったことを思い出すと、「定常分布として事後分布を持つようなマルコフ連鎖を構築する」というのは、「定常分布として事後分布を持つマルコフ連鎖となるように、遷移核を設計する」ことに他なりません。サンプリングしたい分布に対して適切な遷移核を設計するのが、MCMCの役割となります。
MCMCには、様々な種類がありますが、ここではメトロポリス-ヘイスティング・アルゴリズム(以下:M-H)を具体例として示したいと思います。
Step 1. t=1として初期値~\theta^{(0)} を設定する。
Step 2. ~\theta^{(t)} の候補~\tilde{\theta} をマルコフ連鎖から生成する。
\tilde{\theta} \leftarrow q(\theta^{(t-1)},\theta).
Step 3. \tilde{\theta}の採択確率を以下の式で計算する。
\begin{aligned} \alpha(\theta^{(t-1)}, \tilde{\theta}) &=\min\biggl (\frac{p(\theta|X)q(\tilde{\theta},\theta^{(t-1)})}{p(\theta^{(t-1)}|X)q(\theta^{(t-1)},\tilde{\theta})},~1\biggl )\\ &=\min\biggl (\frac{p(X|\theta)p(\theta)q(\tilde{\theta},\theta^{(t-1)})}{p(X|\theta^{(t-1)})p(\theta^{(t-1)})q(\theta^{(t-1)},\tilde{\theta})},~1\biggl ) \end{aligned}
Step 4. \theta^{(t)}を以下のルールに従い更新する。(\mathcal{U}(0,1)は一様分布)
\tilde{u} \leftarrow \mathcal{U}(0,1)
\theta^{(t)} = \begin{cases} \tilde{\theta}, & (\tilde{u}\leqq \alpha(\theta^{(t-1)}, \tilde{\theta})). \\ \theta^{(t-1)}, & (\tilde{u}\geq \alpha(\theta^{(t-1)}, \tilde{\theta})). \end{cases}
Step 5. tを1つ増やしてStep 2.に戻る
Step 2.の遷移核~q(,)には条件がありますが、ここではなんでも良いということにします。
ここで重要な点が2つあります。
- このアルゴリズムは1つ前の要素\theta^{(t-1)}から \theta^{(t)}への移動ルール(遷移核)K(,)を明記しているという点です。
具体的な説明は省略しますが、このアルゴリズムの遷移核K(,)は「定常分布として事後分布を持つマルコフ連鎖となるよう遷移核」であることが示せます。(この部分を深く知りたい方は、「詳細釣り合い条件」について調べてみてください。)ちなみに、遷移核q(,)とM-Hの遷移核K(,)は異なるものなので注意してください。 - Step 3.の\alphaの計算の際に、 p(X)の計算を必要としていない点です。
最初に述べたように、事後分布を解析的に求められない原因は、p(X)を求める際の積分計算が解析的に実行できない点でした。そのため、 p(X)を必要としない点は、極めて重要な性質です。
このように、M-Hなどのアルゴリズムを用いると、事後分布を定常分布とするマルコフ連鎖を構築することができ、このマルコフ連鎖の各要素を近似的に事後分布からのサンプルと見なすことができました。これらのサンプルを用いれば、事後分布の平均・分散などの各種統計量を近似的に計算することができ、具体的な形状を知ることができます。