
概要
この記事では, 「効果検証入門」のポイントをまとめ, 書籍内で行われている分析を掲載していきます.
(本記事は自分が勉強したことのまとめ的要素が強いので, 手元に書籍がある状態でお読みいただくことをオススメします)
尚, 分析コードについては著者が提供しているGitHubからダウンロードもできますので, 実際に手を動かしてみたい方は参考にしてください.
今回は第5章 回帰不連続デザインについて取扱います.(P163~P184が該当)
過去のブログについては以下をご参照ください.
- 第1章 RCTについてはこちら
- 第2章 回帰分析の前半についてはこちら
- 第2章 回帰分析の後半についてはこちら
- 第3章 傾向スコアについてはこちら
- 傾向スコアの発展的な内容は弊社別担当者が執筆したこちらをどうぞ
- 第4章 DIDとCausal Impactについてはこちら
はじめに
まず最初に回帰不連続デザインのざっくりとしたイメージをご説明するために医療費を例に挙げてみます.
基本的に日本では現状, 70才未満は3割, 70才以上は2割, 75才以上は1割の医療費自己負担が発生します. ここで一つの仮説として70才以上になると医療費の自己負担も下がるし, 医療機関の受診回数が増えるのではないかと考えます. もちろん歳をとればとるほど病院に通う回数は増えるでしょうが, 仮に同じくらいの健康状態の人がいるとして, 69才11ヶ月と70才1ヶ月ではそれほど健康状態に差が出るとは考えにくいです. よって, もし実際に70歳前後で受診回数が増えていたとしたらこれは自己負担比率の変化が原因の一つではないかと考えられるわけです. こうした, サンプルが意図せずとも発生する介入付近のデータから効果を推定するのがRDDのアイデアです。
(この例は「データ分析の力 因果関係に迫る思考法 第3章」より引用させていただきました)
ルールが生み出すセレクションバイアス(P164~P166)
明確なルールによって介入が行われる場合, そのルールを満たす場合は必ず介入が発生し, 満たされない場合は必ず介入が発生しない.
このとき用いられるのが回帰不連続デザインである.
回帰不連続デザインのしくみ
- メール配信を例にとる
- 昨年の購買額(history)がある値を超えた場合メールが配信され, そうでない場合はメールが配信されないとする
- ここでメール配信の有無は昨年の購買額のみで決定されるとする→これが介入を決定する係数であり, running valuableと呼び, 閾値(境界となる値)をカットオフと呼ぶ
- ここでカットオフ付近のデータは似た値となっているので, 同質のユーザが集まっていると考え, バイアスをなるべく小さくしている
集計によるセレクションバイアスの確認
- 単純に集計した場合の問題点を考えていく
- 介入グループと非介入グループの平均を比較してしまうと, 本来推定したい効果に潜在的な購買量がプラスされてしまう
- 介入グループは元々昨年の購買量が多かったユーザなので潜在的な購買量とも強い相関があると考えられる
- したがって効果が過剰推定されてしまう恐れがある
回帰不連続デザイン(RDD) (P167~P174)
介入を決定しているものは昨年の購買額(history)なので, これをコントロールできればバイアスが取り除けると考えることができる
線形回帰による分析
- メール配信が目的変数であるサイト来訪者をどの程度増やしたかを推定するにあたり, historyが目的変数と線形関係にあるとすると以下のような回帰式になるY = \beta_0+\beta_1history+\rho Z+u
- ただしρは介入効果を表すパラメータ, Zは介入の有無とする
- もちろん線形の関係でなければセレクションバイアスが発生する
非線形関係による分析
- historyと目的変数が非線形の関係にある場合, それを考慮した回帰モデルが必要であるY = \beta_0+f(X)+\rho Z+u
- 例えば上記のようなべき乗を利用したモデルがある. このときpは自由に設定可能.(かといってやみくもに次数を増やすとモデルが複雑化しすぎてしまう)
メールによる来訪率の増加効果を分析する
- 昨年の購買量(history)の対数が5.5以上($244以上)であればメール配信するとし, サイト来訪を増加させる効果について検証する
# ライブラリの読込
library(tidyverse)
library(broom)
# データの取得
email_data <- read_csv("http://www.minethatdata.com/Kevin_Hillstrom_MineThatData_E-MailAnalytics_DataMiningChallenge_2008.03.20.csv")
# データの整形
## 男性のみのデータにする
male_data <- email_data %>%
## %in%内のどちらかがtrueであればtrue
filter(segment %in% c("Mens E-Mail","No E-Mail")) %>%
mutate(treatment = if_else(segment == "Mens E-Mail", 1, 0),
history_log = log(history))
# データの可視化
male_data %>%
## history_logを小数第1位で丸める
mutate(history_log_grp = round(history_log, 1)) %>%
group_by(history_log_grp, segment) %>%
## 平均来訪率を集計
summarise(visit = mean(visit),
N = n()) %>%
filter(N > 10) %>%
ggplot(aes(y = visit,
x = history_log_grp,
shape = segment,
size = N)) +
geom_point() +
ylim(0,NA) +
theme_bw() +
xlab("log(history)") +
theme(plot.title = element_text(hjust = 0.5),
legend.position = "bottom",
plot.margin = margin(1,2,1,1, "cm"))
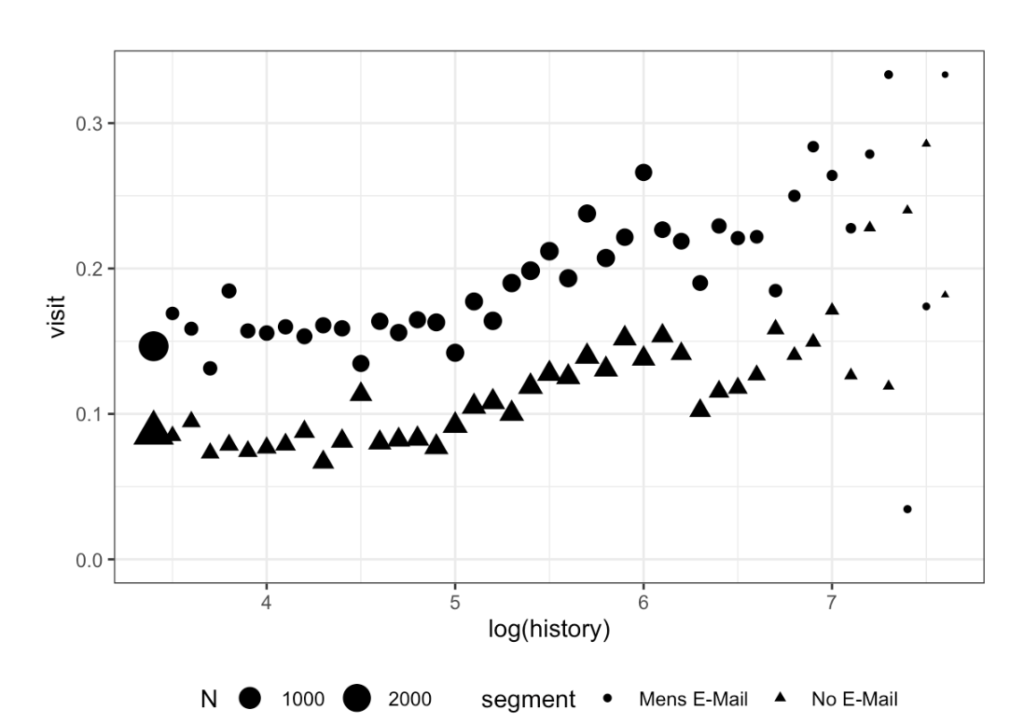
- カットオフ近辺(x=5~6)で来訪率が大きく変化している傾向が見られる
-
次にRDDの設定を行う
- log(hisotry)が5.5以上でメールを受け取ってないデータを, 5.5以下でメールを受け取っているデータを、それぞれ削除する
## カットオフ値の設定
threshold_value <- 5.5
# RDDデータの作成
rdd_data <- male_data %>%
mutate(history_log_grp = round(history_log, 1)) %>%
## 条件にマッチしたデータだけ抜き出す
filter((history_log > threshold_value) & (segment == "Mens E-Mail") |
(history_log <= threshold_value) & (segment == "No E-Mail"))## グラフで確認してみる
rdd_data %>%
group_by(history_log_grp, segment) %>%
## 平均来訪率を集計
summarise(visit = mean(visit),
N = n()) %>%
filter(N > 10) %>%
ggplot(aes(y = visit,
x = history_log_grp,
shape = segment,
size = N)) +
geom_point() +
ylim(0,NA) +
geom_vline(xintercept = threshold_value, linetype = 3)+
theme_bw() +
xlab("log(history)") +
theme(plot.title = element_text(hjust = 0.5),
legend.position = "bottom",
plot.margin = margin(1,2,1,1, "cm"))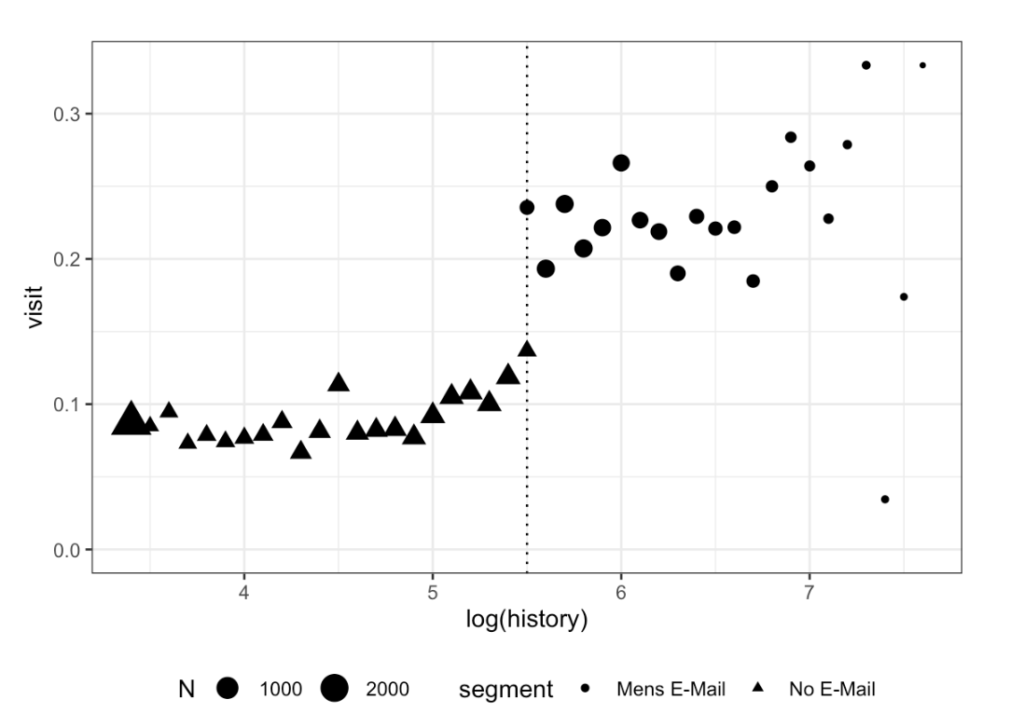
- やはりカットオフ値周辺で来訪率の大きな変化が起きているように思われる
-
次に集計による分析を行う
# RCTデータ ## カットオフ付近の効果 rct_data_table <- male_data %>% filter(history_log > 5, history_log < 6) %>% group_by(treatment) %>% summarize(count = n(), visit_rate = mean(visit)) rct_data_table
- 介入グループの効果は20%程度, 非介入グループは12%程度なので, 8%程度の効果が推定される
# RDDデータ rdd_data_table <- rdd_data %>% group_by(treatment) %>% ## treatmentを集計し, 平均来訪率を算出する summarize(count = n(), visit_rate = mean(visit)) rdd_data_table
- 介入グループは22.4%, 非介入グループは9%程度のため, 13.4%程度の介入効果があると考えられる
- RCTデータでは8%程度の効果が算出されているので, 結果は乖離している. これは昨年の購買量が多い場合, 元々サイトに来訪しやすい状態にあるからである
-
線形回帰分析を実行してみる
rdd_lm_reg <- rdd_data %>% mutate(segment == if_else(segment == "Mens E-Mail", 1, 0)) %>% lm(data = ., formula = visit ~ treatment + history_log) %>% tidy() %>% filter(term == "treatment") rdd_lm_reg
- 介入の効果は約11%程度となり, 集計による分析よりはRCTに近づいた.これはlog(history)の線形の関係による影響を取り除けたためと考えられる
- 今回のようになんらかのルールで介入が割り振られている場合, カットオフ付近のデータだけが利用されていることになるため, 推定結果もカットオフ周辺の効果(Local Average Treatment Effect : LATE)である
-
非線形回帰分析を実行する
- 本書で使用されているrddtoolsパッケージはCRANから削除されてしまったようなので, githubからインストールする必要がある
## rddtoolsをgithubからインストールするためのパッケージ library(remotes) ## パッケージのインストール remotes::install_github("bquast/rddtools") library(rddtools) nonlinear_rdd_data <- rddtools::rdd_data(y = rdd_data$visit, x = rdd_data$history_log, cutpoint = 5.5) ## orderでべき乗を指定できる nonlinear_rdd_ord4 <- rdd_reg_lm(rdd_object = nonlinear_rdd_data, order = 4) nonlinear_rdd_ord4
- 7.4%程度の介入効果が推定されており, RCTの結果である8%にかなり近づいた
nonparametric RDD(P175~P179)
Rによるnonparametric RDDの実装
-
カットオフ付近のデータに限定して分析を行う
- ここでは回帰分析を用いるが, 利用するモデルは非線形を仮定している
- RDesitmateによって最適なバンド幅を推定してくれている
- バンド幅の推定にはクロスバリデーションを用いている
# パッケージのインストール library(rdd) # nonparametric RDDの実行 rdd_result <- RDestimate(data = rdd_data, formula = visit ~ history_log, cutpoint = 5.5) summary(rdd_result)
- Half-BWとDouble-BWはバンド幅をそれぞれ半分, 2倍にした場合の結果である. 幅を小さくした方がバイアスは小さくなる傾向にあるが, その分サンプルサイズが小さくなって標準誤差が大きくなってしまう.
- ただしここではそれほどLATEと推定値が変わっていないので通常のバンド幅でバイアスは小さくなっていると考えられる
-
結果を可視化する
plot(rdd_result) abline(v = 5.5, lty=2)
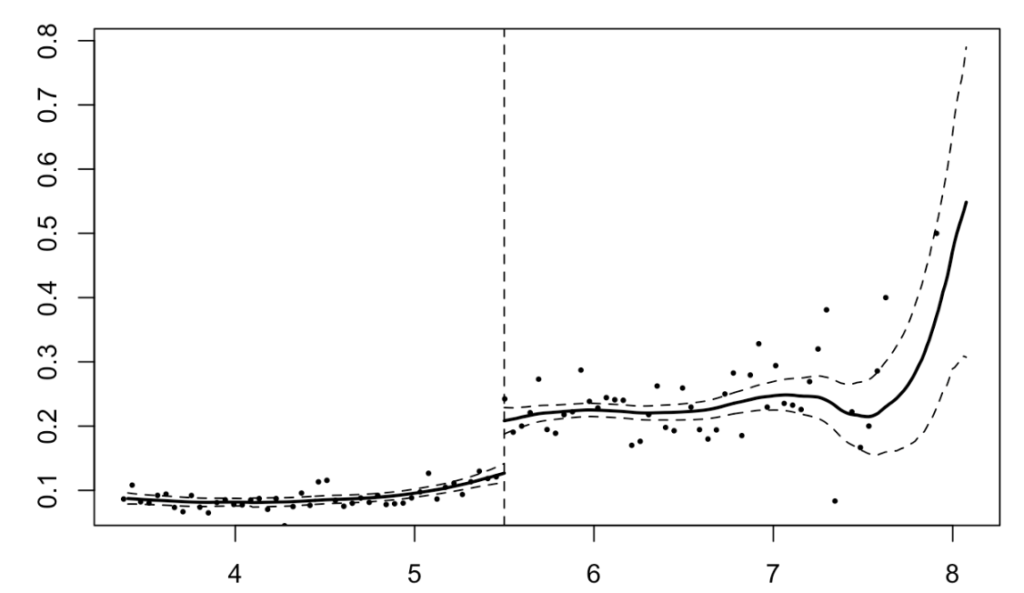
- 横軸が5.5の付近でジャンプしていることがわかる. RDDの結果はこのジャンプの大きさということになる
回帰不連続デザインの仮定(P179~P181)
Continuity of Conditional Regression Functions
- RDDにおいてはContinuity of Conditional Regression Functionsがという仮定が満たされている必要がある
- この仮定は別の介入が発生していると満たされにくい. 例えばメール配信と同時にネット広告も実施してしまうとカットオフ付近で両方の効果が含まれてしまう
non-manipulation
- RDDでは分析の対象が自身の介入に関するステータスを調整できないnon-manipulationという仮定が満たされていることも重要である
- 例えばユーザサイドがある一定額以上購入したら割引券がもらえることがわかっていると意図的に購入額が増えてしまう可能性があり, 推定される効果にユーザの選択というバイアスが含まれてしまう
-
こういった状況が発生しているかを
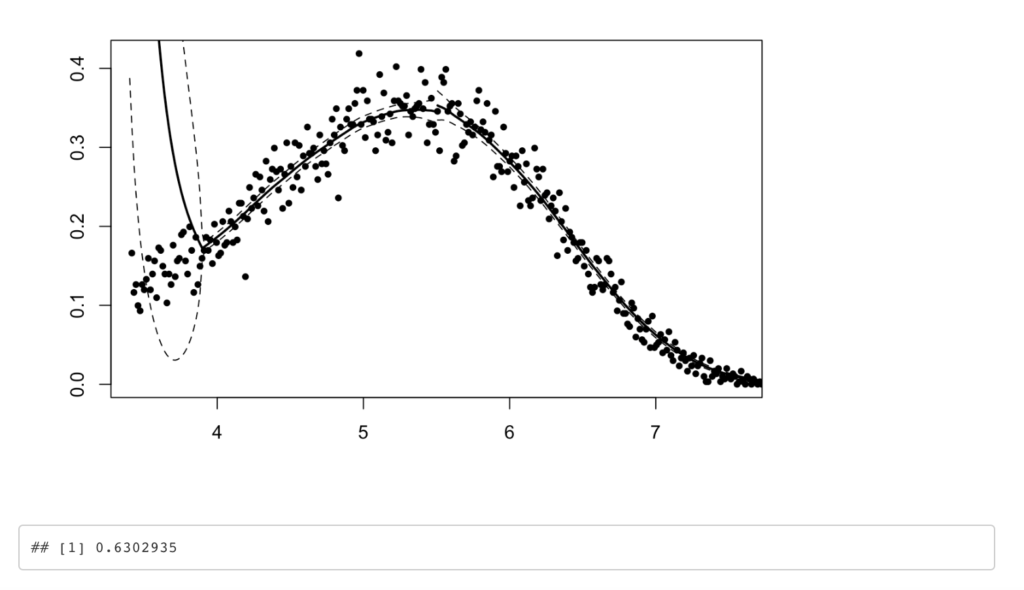
rddパッケージで確認できるDCdensity( ## 密度曲線 runvar = rdd_data %>% pull(history_log), ## カットオフ値 cutpoint = 5.5, plot = TRUE)
- もしp値から有意な結果が得られた場合, 対象者が自身の処置について操作可能な状態となってしまう.(カットオフ付近で密度関数に不連続性がありそうな場合) ここではp値は0.63となっているので, 自分の意思で介入グループに入ることのできる状態とは考えにくい
LATEの妥当性
- RDDの結果はカットオフ付近の効果を推定していることになる.
- もしデータ全体の平均的な効果を考えたい場合はrunning variable(今回の例ではhistory)では介入効果は変化しないという仮定を置かなければならないが, データからは導けないため分析者の解釈に依存する
おわりに
今回のRDDで効果検証入門の書籍内で取り上げられている手法は全てになります. どうやってバイアスを取り除き正しく効果を推定するのか基本的な考えを理解する助けに少しでもなれば幸いです. また自分自身もこうして勉強したことをブログにまとめることで深く理解することに繋がりました.
しかしこれ以外にも考慮すべき点や分析手法はまだまだあります. ここで一旦連載は終了となりますが, 今後も効果検証や実証分析に関するブログは定期的に掲載していきたいと思います.
今までご購読いただいたみなさんありがとうございました!!





![[Rによる演習付き]操作変数法を理解する](https://blog.deepblue-ts.co.jp/wp-content/uploads/writing-828911_1920.jpg)