概要
この記事では, 「効果検証入門」のポイントをまとめ, 書籍内で行われている分析を掲載していきます.
(本記事は自分が勉強したことのまとめ的要素が強いので, 手元に書籍がある状態でお読みいただくことをオススメします)
尚, 分析コードについては著者が提供しているGitHubからダウンロードもできますので, 実際に手を動かしてみたい方は参考にしてください.
今回は第4章 DIDとCausalImpactについて取扱います.(P134~P162が該当)
まず前半部分でDID(差分の差分法)とCausalImapctの考え方を紹介し, 後半部分で演習を行いそれぞれの手法の結果を比較します.
過去のブログについては以下をご参照ください.
- 第1章 RCTについてはこちら
- 第2章 回帰分析の前半についてはこちら
- 第2章 回帰分析の後半についてはこちら
- 第3章 傾向スコアについてはこちら
- 傾向スコアの発展的な内容は弊社別担当者が執筆したこちらをどうぞ
4.1 DID(差分の差分法)(P134~P147)
DIDが必要になる状況
- ある地域で何らかの介入(広告配信, 条例の施行など)があった際に, ほかの地域を非介入グループとして扱い, 介入前後の比較を行いたいが, 地域特性がバイアスとして発生してしまう
- それに対する解決策の一つとしてDIDを導入する
集計による効果検証とその欠点
地域ごとの複数時期のデータが手に入った場合, 以下2つの集計がまず考えられるが, 何かしらのバイアスが発生してしまう
-
介入があった地域となかった地域で比較
- 本来の介入効果+地域固有の効果も含まれてしまう
-
同じ地域の介入前後を比較
- 介入がない場合でも時期的な要因などで自然に増加・減少することもあり, 介入以外の要因を排除できない
DIDのアイデアを用いた集計分析
ここではコレラの感染源特定に貢献したジョンスノウの分析を取り上げる
-
コレラの感染源は水にあると仮定し, 水の供給源で介入グループと非介入グループを分け, それぞれ前後比較を行いその結果の差を見る
-
1849年時点ではSouthwark and Vauxhall社もLambeth社もテムズ川を水源としていたが, 1854年ではLambeth社は他の水源に変わっている. もしコレラの感染源が水源であればLambeth社から水をとっている地域は死者が減少すると考えられる
会社 1849年 死者 1854年死者 Southwark and Vauxhall 2,261 2,458 Lambeth 162 37 Southwark and Vauxhall & Lambeth 3,905 2,547 - 表よりSouthwark and Vauxhall社は増加傾向に, Lambeth社は減少傾向にあることがわかる. また, 両方から取っている地域も減少傾向にあることがわかる
- ここで, もしもLambeth社も水源を変更しなかった場合, Southwark and Vauxhall社と同様に増加傾向になっていれば水源が原因の一つと考えることができる→平行トレンド仮定
-
水源の影響, つまり介入の効果\tauは介入があったエリア内での差分と介入がなかったエリア内の差分の差分で求まる(なので差分の差分法). よって, 介入効果の式は
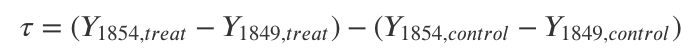
- 実際にRでの集計を行う. ジョンスノウの論文よりデータは作成できる
## 1849年におけるエリア毎のコレラによる死者数
### Southwark and Vauxhall
sv1849 <- c(283,157,192,249,259,226,352,97,111,8,235,92)
### Lambeth Company & Southwark and Vauxhall
lsv1849 <- c(256,267,312,257,318,446,143,193,243,215,544,187,153,81,113,176)
## 1849年におけるエリア毎のコレラによる死者数
### Southwark and Vauxhall
sv1854 <- c(371, 161, 148, 362, 244, 237, 282, 59, 171, 9, 240, 174)
### Lambeth & Southwark and Vauxhall
lsv1854 <- c(113,174,270,93,210,388,92,58,117,49,193,303,142,48,165,132)
## コレラの死者数を会社ごとにまとめる
sv_death <- c(sv1849, sv1854)
lsv_death <- c(lsv1849, lsv1854)
## エリア番号をつける(paste0は結合時に空白ができない)
sv_area <- paste0("sv_",c(1:length(sv1849), 1:length(sv1854)))
lsv_area <- paste0("lsv_", c(1:length(lsv1849), 1:length(lsv1854)))
## どのデータがどの年のものか(repで年数を生成)
sv_year <- c(rep("1849",length(sv1849)), rep("1854", length(sv1854)))
lsv_year <- c(rep("1849",length(lsv1849)), rep("1854", length(lsv1854)))
## Southwark & Vauxhallのデータフレームを作成
sv <- data.frame(area = sv_area,
year = sv_year,
death = sv_death,
LSV = "0",
company = "Southwark and Vauxhall")
## Lambeth & Southwark and Vauxhallのデータフレームを作成
lsv <- data.frame(area = lsv_area,
year = lsv_year,
death = lsv_death,
LSV = "1",
company = "Lambeth & Southwark and Vauxhall")
## SVとLSVを結合(LSVを介入とする)
JS_df <- bind_rows(sv, lsv) %>%
mutate(LSV = if_else(company == "Lambeth & Southwark and Vauxhall", 1, 0))
## 会社別のデータセットを作成
### 会社名, 介入, 年度でグループ化し, 死者数の合計を算出
JS_sum <- JS_df %>%
group_by(company, LSV, year) %>%
summarise(death = sum(death))
## 集計による推定
JS_grp_summary <- JS_sum %>%
### 年度の列を追加
mutate(year = paste("year", year, sep = "_")) %>%
### 横長のデータに変換する
pivot_wider(names_from = year, values_from = death) %>%
mutate(gap = year_1854 - year_1849,
gap_rate = year_1854/year_1849 - 1)
JS_grp_summary
- よって, この分析による効果量は-1357-197=-1554もしくは-43%となる
- 更に, 可視化するとより結果の解釈が容易となる.
## ggplotによる可視化
did_plot <- JS_sum %>%
ggplot(aes(y = death, x = year, shape = company)) +
geom_point(size = 2) +
geom_line(aes(group = company), linetype = 1) +
ylim(2000, 4250) +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5),
legend.position = "bottom",
plot.margin = margin(1,1,1,1, "cm"))
## ggplotによる可視化(アノテーションを追加)
did_plot +
annotate("text", x = 2.2, y = 2400, label = "(1)") +
annotate("text", x = 2.2, y = 3904 + 197*0.6, label = "(2)") +
annotate("text", x = 2.2, y = 3300, label = "(3)") +
annotate("segment", # for common trend in treatment group
x = 1, xend = 2,
y = 3904, yend = 3904 + 197,
arrow = arrow(length = unit(.2,"cm")),
size = 0.1,
linetype = 2) +
annotate("segment", # for parallel trend
x = 1, xend = 2,
y = 2261, yend = 2261,
size = 0.1,
linetype = 2) +
annotate("segment", # for parallel trend
x = 1, xend = 2,
y = 3904, yend = 3904,
size = 0.1,
linetype = 2) +
annotate("segment", # for (1)
x = 2.07, xend = 2.07,
y = 2261, yend = 2458,
arrow = arrow(ends = "both",
length = unit(.1,"cm"),angle = 90)) +
annotate("segment", # for (2)
x = 2.07, xend = 2.07,
y = 3904, yend = 3904 + 197,
arrow = arrow(ends = "both",
length = unit(.1,"cm"),angle = 90)) +
annotate("segment", # for (3)
x = 2.07, xend = 2.07,
y = 3904, yend = 2547,
arrow = arrow(ends = "both",
length = unit(.1,"cm"),angle = 90))
- 仮に平行トレンドが満たされているならば介入グループでも(1)だけ死者数が増加することになる(これは(2)に示されている)
- よって(2)と(3)を足し合わせた分が効果量となる
回帰分析を利用したDID
-
コレラによる死者数を目的変数として, 地域効果(LSV)と共通する時間変化(D53)で回帰モデルを作るY_i = \beta_0 + \beta_1LSV_i+\beta_2D53_i+\beta_3LSV_i*D53_i+u_i
- ここでLSV*D53=1となった場合に介入が発生したことになる
## 回帰分析を実行する
JS_did <- JS_sum %>%
## 時間ダミー
mutate(D1854 = if_else(year == 1854, 1, 0)) %>%
lm(data = ., death ~ LSV + D1854 + D1854:LSV) %>%
tidy()
JS_did
- 結果としては先程と一緒になっている
- 次に地域別データで確認する
## エリア単位での推定
JS_did_area <- JS_df %>%
mutate(D1854 = if_else(year == 1854, 1, 0)) %>%
lm(data = ., death ~ LSV + area + D1854 + D1854:LSV) %>%
tidy() %>%
filter(!str_detect(term, "area"))
JS_did_area
- 各地域およそ100人程度介入効果があるとわかる
- ただしエリアごとで人口も異なるため, ここでは比率をみた方が適切である. よって, 対数をとってもう一度計算してみる
JS_did_area_log <- JS_df %>%
mutate(D1854 = if_else(year == 1854, 1, 0)) %>%
lm(data = ., log(death) ~ LSV + area + D1854 + D1854:LSV) %>%
tidy() %>%
filter(!str_detect(term, "area"))
JS_did_area_log
- 各地域57%程度減少したと推定できる
DIDにおける標準誤差
-
今回扱うデータのように同一のサンプルから複数期間情報を取得したようなパネルデータは自己相関を持つ可能性がある
- 例えばある1店舗のアイスの売り上げを観測したときに, 8/1と8/2では暑いので同じくらいたくさん売れるが, 12/1と12/2では寒いので同じくらいあまり売れないかもしれない.
-
こうしたデータの場合, 標準誤差が過少に算出されてしまうため, クラスター標準誤差という観測対象ごとの誤差を用いた回帰分析を行うことが望ましい
- Rではmiceaddsパッケージの
lm.clusterやestimatrパッケージのlm_robustを用いることで実行可能
- Rではmiceaddsパッケージの
平行トレンド仮定と共変量
-
ここまでの分析では, Lambeth社が水源変更をしなかった場合, Southwark and Vauxhall社と同様にコレラによる死者数が増加しているという平行トレンド仮定を置いている
- しかし基本的にはデータを用いた確認をすることは難しい
- ある程度長い期間データを観測すれば周期性や類似度を確認できるが, 介入前の期間が複数必要になるため, なかなか明確な傾向を掴むことはできない
-
対策としては以下の2つが挙げられる
-
仮定を満たさないと考えられるデータから取り除く
- 介入エリアの近隣のデータを取得するなどの工夫が必要
- 介入のタイミングより前のデータからトレンドが同じになるようなサンプルを自動検出する合成コントロール法も存在する
-
共変量としてトレンドの乖離を説明するような変数をモデルに加える
- 例えば水質を改善するような施設がどこかで作られれば平行トレンドは成り立たなくなるが, これを共変量に入れ込めば施設の効果は介入効果のパラメータからは取り除ける
-
仮定を満たさないと考えられるデータから取り除く
4.2 CausalImpact(P147~P150)
DIDの欠点
-
分析の際, 複数の地域や時間でデータを取得している必要がある
-
どのデータを分析に用いるか担当者の仮説に依存する
- 平行トレンド仮定を満たすようなデータ取得や共変量の調整が必要
CausalImpactのアイデア
-
CausalImpactではさまざまな変数Xを用いて, 目的変数Yを予測するモデルを介入が行われる前の期間のみで作成する
-
ここで変数Xには検索回数やアクセス数などを盛り込め, 変数も自動的に選択をしてくれる
- 結果として介入後のXのデータを代入することで介入がなかった場合のYの値を算出し, これと実際の介入後との結果の差分をとることで効果を測定することができる
- ただし, CausalImpactにおいても平行トレンド仮定は重要であり, どのデータをそもそも使うべきかは分析者の判断に委ねられる
-
4.3 大規模禁煙キャンペーンがもたらすタバコの売上への影響(P150~P160)
1988年からカリフォルニアでは大規模な禁煙キャンペーンとしてタバコ増税が実施された. この介入がどの程度タバコの消費に影響を与えたかをDIDとCausalImpactで検証し, 結果を比較していく. この介入はカリフォルニア州全体で行われたため, その他の州との比較をする必要がある
データの準備
- Ecdatパッケージ内のCigarデータセットを用いる. このデータには全米各州の人口1人あたりのタバコの売上が記録されている. ただしカリフォルニアと同様に一定水準以上の増税があった州は分析から除外し, さらに1970年\~1992年を分析対象とする
## 使用するデータが含まれるパッケージ
library(Ecdat)
## 除外する州のリスト
skip_state <- c(3, 9, 10, 21, 22, 23, 31, 33, 48)
## 分析データの作成
Cigar <- Ecdat::Cigar %>%
## skip_stateで指定した州を除外
filter(!state %in% skip_state,
year >= 70) %>%
mutate(area = if_else(state == 5, "CA", "Rest of US"))DIDの実装
Cigar %>%
mutate(period = if_else(year > 87, "after", "before"),
state = if_else(state == 5, "CA", "Rest of US")) %>%
group_by(period, state) %>%
## グループごとの一人当たり売上を算出
summarise(sales = sum(sales*pop16)/sum(pop16)) %>%
pivot_wider(names_from = state, values_from = sales)

## 可視化
Cigar_plot <- Cigar %>%
mutate(period = if_else(year > 87, "after", "before"),
state = if_else(state == 5, "CA", "Rest of US")) %>%
group_by(period, state) %>%
summarise(sales = sum(sales*pop16)/sum(pop16)) %>%
ggplot(aes(y = sales, x = period, shape = state)) +
geom_point(size = 2) +
geom_line(aes(group = state, linetype = state)) +
ylim(50, 150) +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5),
legend.position = "bottom",
plot.margin = margin(1,1,1,1, "cm"))+
### 軸の順番を調整できる
scale_x_discrete(name = "Period", limits = c("before", "after"))
Cigar_plot
- CAでは40箱程度, その他では20箱程度減少したとわかるので, 大体20箱程度の減少が介入効果として想定される
-
次にDIDを以下の回帰式を想定して推定する
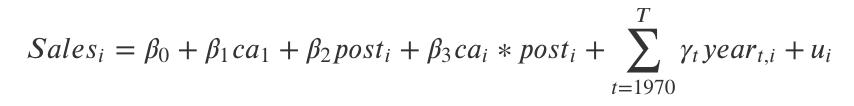
- ここで, caはカリフォルニア州かどうか, postは介入が行われた期間かどうか, yearは年度ごとの固有効果をあらわす
## カリフォルニア州とその他, 介入前後でわける
Cigar_did_sum <- Cigar %>%
mutate(post = if_else(year>87, 1, 0),
ca = if_else(state == 5, 1, 0),
state = as.factor(state),
year_dummy = paste0("D_", year)) %>%
group_by(post, year, year_dummy, ca) %>%
summarise(sales = sum(sales*pop16)/sum(pop16))
## 回帰分析
Cigar_did_sum_lm <- Cigar_did_sum %>%
lm(sales ~ ca + post + ca:post + year_dummy,
data = .) %>%
tidy() %>%
filter(!str_detect(term, "year"))
Cigar_did_sum_lm
- 約20箱程度の削減効果が推定された
-
次に比率での効果を確認する
## 回帰分析(比率で算出) Cigar_did_sum_lm_log <- Cigar_did_sum %>% lm(log(sales) ~ ca + post + ca:post + year_dummy, data = .) %>% tidy() %>% filter(!str_detect(term, "year")) Cigar_did_sum_lm_log
- 25%程度減少されたことがわかる
-
そもそも平行トレンドを満たしているのかを確認してみる
Cigar_did_sum %>% mutate(state = if_else(ca == 1, "CA", "Rest of US")) %>% ggplot(aes(x = year, y = sales, shape = state))+ geom_point(size = 1.5)+ geom_line(aes(linetype = state))+ geom_vline(xintercept = 88, linetype = 3)
- カリフォルニアとそれ以外でトレンドに差異があると見られる(平行ではなさそう)
CausalImpactの実装
-
目的変数Y, 予測に利用する変数X, 介入期間を表す変数を入力する. この時Xは今までとは異なり平行トレンドを満たすような変数である.
- ここで使用するXはカリフォルニア以外でのタバコの売上とする
# CausalImpactの実装 library(CausalImpact) ## 目的変数(カリフォルニアの売上) Y <- Cigar %>% filter(state == 5) %>% pull(sales) ## 共変量 X_sales <- Cigar %>% filter(!state == 5) %>% dplyr::select(state, year, sales) %>% tidyr::pivot_wider(names_from = state, values_from = sales) ## 介入前の期間と介入後の期間を設定 ### 今回は23年間のうち5年間が介入後 pre_period <- c(1:nrow(X_sales))[X_sales$year < 88] post_period <- c(1:nrow(X_sales))[X_sales$year >= 88] ## データ結合 CI_data <- cbind(Y, X_sales) %>% dplyr::select(-year) ## CausalImpactの実行 ### periodの部分で介入前後を指定 impact <- CausalImpact(data = CI_data, pre.period = c(min(pre_period), max(pre_period)), post.period = c(min(post_period), max(post_period))) plot(impact)
- originalはカリフォルニアのタバコの売上とそれに対する予測値となっており, 実線が実際の売上, 点線が予測値
- 介入のあったタイミングで実線と点線がズレ始めている
- pointwiseはoriginalにおける実線と点線のズレをプロットしたもの
- cumulativeはpointiwiseのグラフを介入が始まったあとから積み上げたもの
- さらに推定された効果を実数と比率で確認する
impact
-
Absolute effectで実際の効果を確認でき, ここでは平均13箱減少したことがわかる(Relative effectでは比率を確認できる)
- 標準誤差は5.5であり, [ ]の中が95%信用区間である
- ここで区間の中に0は含まれていないので, 効果が0である可能性は低そうである
分析結果の比較
-
今回の分析の元となる論文では合成コントロールという手法を用いている. これは仮に介入対象地域が何らかの介入を行っていた場合にどうなっていたのかを、他地域のデータを合成値とすることによって予測する手法である.
- 抽出する地域は人口や経済状況などが比較的似ている地域とすることで平行トレンドを満たしていると仮定する
- 実際の論文では1988年からタバコの売上は徐々に減少し, 1992年までに15箱程度の減少, その後1995年まで効果が強まり, 20箱程度が減少したとされている
- DIDは少し過剰に推定され, CausalImpactではある程度類似した結果となった
4.4 不完全な実験を補佐する(P160~P162)
DIDやCausalImpactは実験上の制約やABテストが不可能な場合などに重宝するが, このアイデアを用いることができない場合もある
DIDのアイデアを用いた分析が使えないとき
-
他の介入が同時に行われてしまったとき
- 例えば, 広告展開と同時に値下げをするとどちらの効果で売上に変化があったかわからない
- 解決策としては共変量に価格を入れてしまうことも可能だが, 同時に何個も介入があるとやはり効果推定はほぼ不可能となってしまう
おわりに
今回の記事ではDIDとCausalImpactをご紹介しました. 基本的な分析の流れはおさえることはできましたが, 途中でご紹介したクラスター標準誤差や合成コントロール法など発展的な内容も実際の分析に応用する際は抑えておく必要があるように感じました.
いよいよ次回は最後のトピックとなる回帰不連続デザイン(RDD)を扱います.
最後までお読みいただきありがとうございました!