はじめに
最近Instagramのおすすめを見る機会が増えたのですが、中でもリールと呼ばれる短い動画を見る時間が多くなっていることに気がつきました。
写真を並べることが多い通常の投稿と比べて、リールはついつい見入ってしまうことが多々あります。
先日もグルメに関するリールを投稿するアカウントをフォローしてしまいました。
そこでリールを投稿することでフォロワー数が増えやすくなるという仮説を立て、統計的因果推論を用いて検証してみました。
使用したデータについて
調査対象は大学やその他団体が主催しているミスター・ミスコンテストに出場している人のアカウントです。
選んだ理由は、フォロワー数を増やすことを目的としており、投稿内容以外の影響を受けてフォロワー数が増加する可能性が低いと考えたからです。
例えば芸能人のSNSアカウントでは、その人が視聴率の高いTV番組に出て注目を浴び、フォロワーが増えるような場合が考えられます。
このような影響を取り除くのは大変なので、投稿内容以外の影響によりフォロワー数が増加する可能性がある有名人やお店などのアカウントはフォロワー数を増やそうとしていると考えられますが避けました。
2021年のコンテスト出場者のうち、私が見つけることができた300前後のアカウントを対象にデータ収集を試みました。
Instagram Graph APIを利用し、正常に情報が取得できたアカウントのデータを収集しました。
収集方法についてはここでは説明を割愛させていただきます。
サンプルサイズは150になり、それらのアカウントのユーザー名とフォロワー数、フォロー数、投稿数を取得しました。
性別とリールを投稿しているかを確認し、二値変数で表現しました。
結果変数はフォロワー数とします。
ただし、本研究では結果変数に外れ値が存在し、また結果変数と共変量のスケールが異なるため、対数変換したフォロワー数を結果変数として解析しています。
フォロー数や投稿数についてもそれぞれの対数を求め、変数として追加しました。
変数名とその内容は以下の表の通りです。
| 変数名 | 内容 |
|---|---|
| followers_count | フォロワー数 |
| log_followers_count | フォロワー数の対数 |
| follows_count | フォロー数 |
| log_follows_count | フォロー数の対数 |
| media count | 投稿数 |
| log media count | 投稿数の対数 |
| sex | 性別 : 1(男性), 0(女性) |
| reel | リールを投稿したか : 1(投稿した), 0(投稿していない) |
収集したデータをcsv形式で保存し、同じフォルダにcsvファイルを置き、以下のようにして読み込みます。
csvファイルはこちらです。
import pandas as pd
data_mrms = pd.read_csv('data.csv', index_col=0)
処置
処置とは、原因となる事柄を実施することです。介入と呼ぶこともしばしばあります。
今回は「リール(動画の一種)を投稿すること」を処置とします。
Z = 1 を処置を意味するダミー変数とし、 Z = 1 となる個体の数を数えます。
# 処置群(Z = 1)と対照群(Z = 0)の個体数
print(data_mrms['reel'].value_counts())
-- Output --
1 120
0 30
Name: reel, dtype: int64
この場合、Z = 1 となる個体の数が120で Z = 0 となるのは30人であることがわかります。
次にそれぞれの群における結果変数の平均を求めます。
# それぞれの群における結果変数(対数)の平均
print(data_mrms.groupby(['reel'])['log_followers_count'].mean())
-- Output --
reel
0 6.901708
1 7.916557
Name: log_followers_count, dtype: float64
処置と結果変数の関係を箱ひげ図に示します。
import matplotlib.pyplot as plt
# 処置と結果変数の関係を示す箱ひげ図
fig, ax = plt.subplots()
ax.boxplot(x=[data_mrms.query('reel == 1')['log_followers_count'], data_mrms.query('reel == 0')['log_followers_count']], labels = [1, 0])
ax.set_xlabel('reel')
ax.set_ylabel('log_followers_count')
ax.set_title('reel and log_followers_count')
plt.show()

共変量の選択
共変量とは結果変数 Y と処置の割り当て Z の両方に影響を与える変数のことです。
今回は処置群と対照群の結果変数の差は約1.015でしたが、この2群の差は必ずしも処置の有無によるものだけではなく他の要因からの影響も含めた結果になります。
ave = data_mrms.groupby(by='reel')['log_followers_count'].mean() # 重み付け前のlogyの平均
print(f'before \nz = 1 : {ave[1]:.3f}\nz = 0 : {ave[0]:.3f}\ndif : {ave[1] - ave[0]:.3f}')
-- Output --
before
z = 1 : 7.917
z = 0 : 6.902
dif : 1.015
適切な変数を選択し、共変量として扱うことで、注目する 2 変数以外の変数の影響を取り除き、因果効果を正しく推定することが期待できます。
得られたデータに多くの変数が存在する場合、どの変数が共変量となりうるか考える必要があります。
今回は以下の選択基準に照らして選びます。
- 処置と結果変数の両方に影響を与える変数を共変量として利用する。
- 処置から影響を受け, 結果変数に影響を与える変数(中間変数)は因果効果を過小評価するので共変量としないことが多い。
- 処置とは独立で結果変数に影響を与える変数は共変量としても良い. 採用した場合としない場合で因果効果は変わらない. ただし推定値の分散が大きくなる恐れがある。
- 処置群と対照群で分布が異なる変数を共変量として利用する。
まず性別と目的変数(フォロワー数)の関係について調べます。
後ほどフォロー数の対数と投稿数の対数についても、それぞれと結果変数や介入との関係を調べることにします。
# 性別と結果変数の関係を示す箱ひげ図
fig, ax = plt.subplots()
ax.boxplot(x=[data_mrms.query('sex == 1')['log_followers_count'], data_mrms.query('sex == 0')['log_followers_count']], labels = ['men', 'women'])
ax.set_xlabel('sex')
ax.set_ylabel('log_followers_count')
ax.set_title('sex and log_followers_count')
plt.show()

箱ひげ図を見るとかなり男女差がありそうです。
つまり性別は結果変数に影響を与えていると考えられます。
性別と介入(リールを投稿する)の関係についても確認しましょう。
分割表を作成します。
table_x1_z = pd.crosstab(data_mrms['sex'], data_mrms['reel'], margins=True)
table_x1_z
| reel | 0 | 1 | All |
|---|---|---|---|
| sex | |||
| 0 | 21 | 77 | 98 |
| 1 | 9 | 43 | 52 |
| All | 30 | 120 | 150 |
独立性の検定を行い、性別と介入の有無が独立であるかを調べます。
帰無仮説 H_0 を「性別と処置は独立である」とし、有意水準を5%に設定します。
chi2 = 0 # カイ二乗統計量の初期値
# カイ二乗統計量を求める
for i in range(2):
for j in range(2):
o = table_x1_z.loc[i, j] # 実測値
e = table_x1_z.loc[i, 'All'] * table_x1_z.loc['All', j] / table_x1_z.loc['All', 'All'] # 理論値
chi2 += (o - e) ** 2 / e
print(f'chi2 = {chi2:.2f}\nchi2 < 3.84 : {chi2 < 3.84}')
-- Output --
chi2 = 0.36
chi2 < 3.84 : True
検定統計量が 3.84 = \chi_{0.05}^2(1) より小さいので有意水準5%で帰無仮説を棄却できない、すなわち独立でないとは言えません。
'log_follows_count' と 'log_media_count' についても、共変量 X として採用すべきか確認します。
これら2変数と目的変数についての相関係数行列を求めます。
data_mrms[['log_followers_count', 'log_follows_count', 'log_media_count']].corr()
| log_followers_count | log_follows_count | log_media_count | |
|---|---|---|---|
| log_followers_count | 1.000000 | 0.428808 | 0.467008 |
| log_follows_count | 0.428808 | 1.000000 | 0.374697 |
| log_media_count | 0.467008 | 0.374697 | 1.000000 |
結果変数と二つの共変量の候補(フォロー数の対数と投稿数の対数)の間にはそれぞれ正の相関があることがわかリます。
このことは次の散布図からも確認できます。
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12,6))
# フォロー数の対数と結果変数の散布図
axs[0].scatter(x=data_mrms['log_follows_count'], y=data_mrms['log_followers_count'])
axs[0].set_xlabel('log_follows_count')
axs[0].set_ylabel('log_followers_count')
axs[0].set_title('log_follows_count and y')
# 投稿数の対数と結果変数の散布図
axs[1].scatter(x=data_mrms['log_media_count'], y=data_mrms['log_followers_count'])
axs[1].set_xlabel('log_media_count')
axs[1].set_ylabel('log_followers_count')
axs[1].set_title('log_media_count and y')
plt.show()

次に処置と二つの共変量の候補(フォロー数の対数と投稿数の対数)の関係について調べましょう。
それらの関係を箱ひげ図に示します。
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
# 処置と投稿数の対数の箱ひげ図
axs[0].boxplot(x=[data_mrms.query('reel == 1')['log_media_count'], data_mrms.query('sex == 0')['log_media_count']], labels = ['men', 'women'])
axs[0].set_xlabel('reel')
axs[0].set_ylabel('log_media_count')
axs[0].set_title('reel and log_media_count')
# 処置と結果変数の箱ひげ図
axs[1].boxplot(x=[data_mrms.query('reel == 1')['log_follows_count'], data_mrms.query('sex == 0')['log_follows_count']], labels = ['men', 'women'])
axs[1].set_xlabel('reel')
axs[1].set_ylabel('log_follows_count')
axs[1].set_title('reel and log_follows_count')
plt.show()

ここまでの結果より、性別とフォロー数の対数、投稿数の対数は全て共変量になりうると考えられます。
そこでこの3変数を説明変数とし、介入の有無を表すダミー変数を結果変数としたロジスティック回帰モデル
P({\tt reel} = 1 \mid \boldsymbol{X}_i) = \frac{1}{1 + \exp\left( -\left( \beta_0 + \beta_1 {\tt sex}_i + \beta_2 {\tt log\_media\_count}_i + \beta_3 {\tt log\_follows\_count}_i \right) \right)}を考えます。
説明変数の p 値が0.05 未満のとき、その説明変数が結果変数に何らかの影響を与えると言えます。
import numpy as np
import statsmodels.formula.api as smf
import statsmodels.api as sm
logistic_model = smf.glm(formula = "reel ~ sex + log_media_count + log_follows_count",
data = data_mrms,
family=sm.families.Binomial(link=sm.genmod.families.links.logit())
)
logistic_result = logistic_model.fit()
logistic_result.summary()
| Dep. Variable: | reel | No. Observations: | 150 |
|---|---|---|---|
| Model: | GLM | Df Residuals: | 146 |
| Model Family: | Binomial | Df Model: | 3 |
| Link Function: | logit | Scale: | 1.0000 |
| Method: | IRLS | Log-Likelihood: | -53.142 |
| Date: | Tue, 15 Mar 2022 | Deviance: | 106.28 |
| Time: | 16:12:24 | Pearson chi2: | 190. |
| No. Iterations: | 6 | Pseudo R-squ. (CS): | 0.2534 |
| Covariance Type: | nonrobust |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -7.2977 | 1.739 | -4.196 | 0.000 | -10.706 | -3.889 |
| sex | 0.7844 | 0.561 | 1.397 | 0.162 | -0.316 | 1.885 |
| log_media_count | 1.9912 | 0.427 | 4.662 | 0.000 | 1.154 | 2.828 |
| log_follows_count | 0.1104 | 0.202 | 0.546 | 0.585 | -0.286 | 0.507 |
従ってこのモデルで有意であると言える変数は投稿数の対数のみです。
以降共変量は 'log_media_count' のみであると考え、この変数による影響を取り除くための手法を用います。
傾向スコア推定
投稿数の対数を共変量として傾向スコアを推定しましょう。
個体 i の傾向スコアは、共変量が与えられたときの処置群に割り当てられる条件付き確率
e_i = P(Z_i = 1 \mid \boldsymbol{X}_i)で定義されます。
しかし、傾向スコアの真の値を観測することはできないので、得られたデータから推定する必要があります。
推定にしばしば用いられるモデルの一つがロジスティック回帰モデルです。
今回もロジスティック回帰モデルを用います。
傾向スコアの推定値は
\hat{e}_i = \frac{1}{1 + \exp\left( -\left( \hat{\beta}_0 + \hat{\beta}_1 {\tt log\_media\_count}_i \right) \right)}から得られます。
係数の推定値はロジスティック回帰モデルを当てはめることで得られます。
import math
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
# シグモイド関数を定義
def func_sigmoid(x):
return 1 / (1 + math.exp(-x))
Z = data_mrms['reel'] # 処置の割付けを表すダミー変数
X = data_mrms['log_media_count'] # 共変量(対数変換した投稿数)
X = X.to_frame()
# ロジスティック回帰
model = LogisticRegression(solver="liblinear")
model.fit(X, Z) # 学習
beta0 = model.intercept_[0] # 切片項
beta1 = model.coef_[0][0] # 回帰係数1
# 傾向スコアを計算
Y = [beta0 + beta1 * X.loc[i, 'log_media_count'] for i in range(len(data_mrms))]
ps = [func_sigmoid(y) for y in Y]
data_mrms['ps'] = ps # データフレームに「傾向スコアの推定値」の列を追加
plt.scatter(X['log_media_count'], ps) # シグモイド関数の形になっているか確認

出力結果は投稿数の対数と傾向スコアの推定値のプロットです。
これを見るとシグモイド関数に近い形になっていることが確認できます(そうでなければ傾向スコアの推定までの過程でミスがある可能性が高いですので見直すべきでしょう)。
逆確率による重み付け(IPW)法
傾向スコアを用いた解析法の一つに逆確率による重み付け法(IPW法)を用いて平均処置効果の推定値を求めます。
平均処置効果のIPW推定量とは、傾向スコアの逆数による重み付け平均の差
\hat{E}[Y_1] - \hat{E}[Y_0] = \frac{\displaystyle\sum_{i = 1}^N \dfrac{Z_i Y_i}{e_i}}{\displaystyle\sum_{i = 1}^N \dfrac{Z_i}{e_i}} - \frac{\displaystyle\sum_{i = 1}^N \dfrac{(1 - Z_i) Y_i}{1 - e_i}}{\displaystyle\sum_{i = 1}^N \dfrac{1 - Z_i}{1 - e_i}}です。
平均処置効果のIPW推定量は「強く無視できる割り当て条件」を仮定した下で、平均処置効果の一致推定量であることが知られています。
ただし、次の2条件を満たすと仮定することを「強く無視できる割り当て条件」と呼びます。
- 処置の割り当てが共変量のみに依存し結果変数に依らない。
- P(Z = 1 \mid \boldsymbol{X}) が0より大きく1より小さい。
# 重みの推定
data_mrms['weight'] = data_mrms[['ps', 'reel']].apply(lambda x: 1 / x[0] if x[1] == 1 else 1 / (1 - x[0]), axis=1)
data_mrms['weight_logy'] = data_mrms[['log_followers_count', 'weight']].apply(lambda x: x[0] * x[1], axis=1)
weight_y = data_mrms.groupby(by=['reel'])['weight_logy'].sum() / data_mrms.groupby(by=['reel'])['weight'].sum() # 重みの和で割ったとき
print(weight_y)
# IPW推定量
ate = weight_y[1] - weight_y[0]
ate
-- Output --
reel
0 6.975394
1 7.889948
dtype: float64
0.9145540484766608
この結果より、平均処置効果の推定値は約0.915であるとわかりました。
先ほどの処置群と対照群の結果変数の差は約1.015でしたので、因果効果が過大評価されていたことがわかります。
IPW推定量の漸近分散に基づく分散の推定値
平均処置効果の IPW 推定量の漸近分散に基づく分散の推定値は
\frac{1}{N^2} \sum_{i = 1}^N \left( \frac{Z_i(Y_i - \hat{E}[Y_1])^2}{\hat{e}_i^2} + \frac{(1 - Z_i)(Y_i - \hat{E}[Y_0])^2}{(1 - \hat{e}_i)^2} \right)で与えられます。
平均処置効果の IPW推定量の推定値と分散の推定値を用いて統計的仮説検定を行います。
帰無仮説を「 H_0 : 処置群と対照群でフォロワー 数に差が生じない」とし、有意水準を 5% とします。
S = 0
for i in range(150):
z = data_mrms.at[i, 'reel']
y = data_mrms.at[i, 'log_followers_count']
e = data_mrms.at[i, 'ps']
S += z * ((y - weight_y[1]) ** 2) / (e ** 2) + (1 - z) * ((y - weight_y[0]) ** 2) / ((1 - e) ** 2)
asymptotic_variance = S / (150 ** 2)
asymptotic_variance
-- Output --
0.01777048382747068
import math
print(f'検定統計量 : {ate / math.sqrt(asymptotic_variance):.2f}\n6.86 > 1.96 : {ate / math.sqrt(asymptotic_variance) > 1.96}')
-- Output --
検定統計量 : 6.86
6.86 > 1.96 : True
従って、帰無仮説は棄却されます。
すなわちリールを投稿するかどうかでフォロワー数に差が生じると言えます。
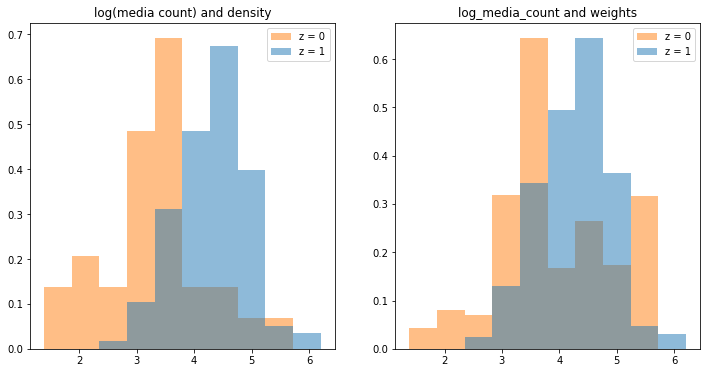
IPW法の前後での分布の比較
次に重みをかけた共変量の密度推定して共変量がバランスしたかを確認します。
X の列に対して、重みをかける前後の密度に関するヒストグラムを並べました。
左が調整前、右が調整後です。
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
# 調整前の投稿数を対数変換したものと確率密度のヒストグラム
axs[0].hist(x=[data_mrms.query('reel == 1')['log_media_count'], data_mrms.query('reel == 0')['log_media_count']], density=True, histtype='stepfilled', alpha = 0.5, label=['z = 1', 'z = 0'])
axs[0].set_title('log(media count) and density')
axs[0].legend()
# 調整後の投稿数を対数変換したものと確率密度のヒストグラム
axs[1].hist(x=[data_mrms.query('reel == 1')['log_media_count'], data_mrms.query('reel == 0')['log_media_count']], density=True, weights=[data_mrms.query('reel == 1')['weight'], data_mrms.query('reel == 0')['weight']], histtype='stepfilled', alpha = 0.5, label=['z = 1', 'z = 0'])
axs[1].set_title('log_media_count and weights')
axs[1].legend()
plt.show()

このヒストグラムを見ると、調整後の2群における投稿数の対数の分布は調整前と比べて重なりが大きくなっています。
すなわち、処置群と対照群の分布の偏りが小さくなっていると言えます。
ライブラリの活用
平均処置効果のIPW推定量の推定値はIBMが公開している causallib というライブラリを使うと簡単に結果が得られます。
興味のある方は活用してみてください。
参考までに結果を載せておきます。
自分で実装した結果と、IPW推定量の推定値がほとんど一致していることがわかります。
from causallib.estimation import IPW
from causallib.evaluation import PropensityEvaluator
from sklearn.linear_model import LogisticRegression
# 目的変数と処置のダミー変数と共変量の変数を用意
Y = data_mrms['log_followers_count'] # 目的変数(対数変換したフォロワー数)
Z = data_mrms['reel'] # 処置の割付けを表すダミー変数
X = data_mrms['log_media_count'] # 共変量(対数変換した投稿数)
X = X.to_frame()
# 学習
learner = LogisticRegression(solver="liblinear")
ipw = IPW(learner)
ipw.fit(X, Z)
# 重みの推定
outcomes = ipw.estimate_population_outcome(X, Z, Y)
# IPW推定量
effect = ipw.estimate_effect(outcomes[1], outcomes[0])
effect
-- Output --
diff 0.914554
dtype: float64
まとめ
投稿数の対数の影響を取り除き、因果効果を推定しました。
その結果リールを投稿する場合は、しない場合と比べてフォロワー数が exp(0.915) = 2.50 倍増加す ると解釈できます。
また仮説検定の結果、これらの差は有意でした。
今回行った調査の課題の一つに「共変量の選択」があります。
今回のような観察研究を行う場合、一般には全ての共変量が観測されていることが求められます。
しかし、自分の収集したデータは十分な種類の変数があったとは言い難いです。
この調査は筆者にとって因果推論の奥深さを知るきっかけになりました。
引き続き学習を進めてまいります。
参考文献
- 星野崇宏 (2009), 調査観察データの統計科学, 岩波書店.
- 安井翔太 (2020), 効果検証入門, 技術評論社.
- 岩波データサイエンス刊行委員会 (2016), 岩波データサイエンス Vol.3, 岩波書店.


