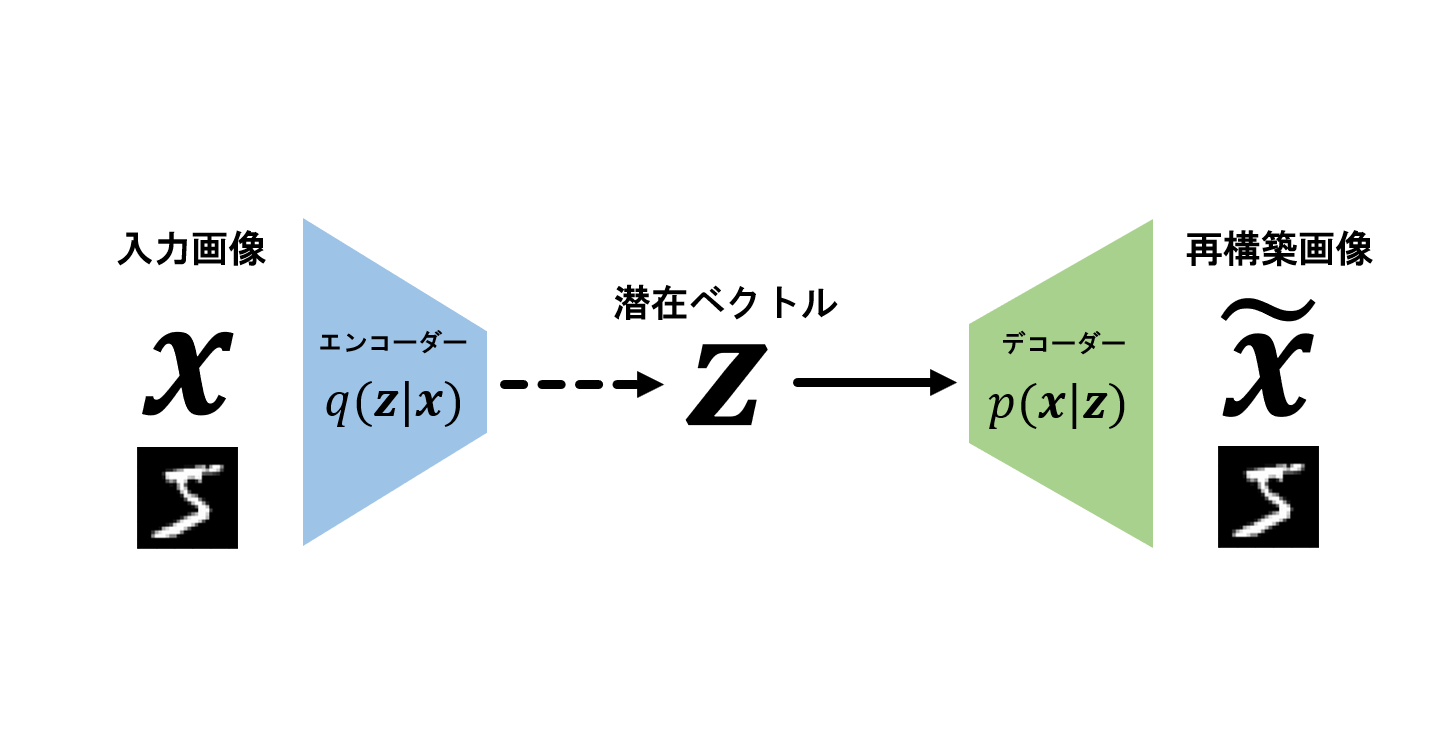
前回はニューラルネットワークの概要について説明しました。
今回は実装する前に順伝播計算などの計算について説明します。

三層ニューラルネットワークのフルスクラッチによる実装①
三層ニューラルネットワークのフルスクラッチによる実装③

順伝播計算

言葉の定義

　まずは説明で利用する言葉と表記を定義します。今回、第三層のニューラルネットワークについて説明しますが一般的な表記で定義します。

X = \{\bm{x_1},\cdots,\bm{x_n}\}
Y = \{\bm{y_1},\cdots,\bm{y_n}\}
D = \{\bm{d_1},\cdots,\bm{d_n}\}

上記は上からデータ、出力、教師データとなります。それぞれの要素\bm{x_i}などはベクトルを表します。

第l層のユニットiについて入力をu_{i}^{(l)}、出力をz_{i}^{(l)}、第l-1層のユニットjから第l層のユニットiへの係数をw_{ij}^{(l)}、第l層のユニットiでのバイアスはb_{i}^{(l)}とします。

　上記の定義より出力は以下のように書けます。

z_{i}^{(l)} = f(u_{i}^{(l)})
u_{i}^{(l)} = \sum_{j=1}^{n}w_{ij}^{(l)}z_{j}^{(l-1)}+b_{i}^{l}
f(・)は活性化関数で、各層ごとに設定します。

ベクトル表記

　まず上記で定義した文字をベクトル表記します

W = \left( \begin{array}{ccc} w_{11} \cdots w_{1m}\\ \vdots \ddots \vdots\\ w_{n1} \cdots w_{nm} \end{array}\right)
\bm{z} = \left( \begin{array}{c} z_{1}\\ \vdots\\ z_{n} \end{array} \right)
\bm{u} = \left( \begin{array}{c} u_{1}\\ \vdots\\ u_{n} \end{array} \right)
\bm{b} = \left( \begin{array}{c} b_{1}\\ \vdots\\ b_{n} \end{array} \right)

　上から係数行列、出力ベクトル、入力ベクトル、バイアスベクトルとなります。以降説明する際は文字定義同様l層目のものはW^{(l)}などと表記します。

順伝播の計算

　順伝播ではデータ入力から出力までを行います。

データのi番目\bm{x_i}が入力されたとします。

　まず、データを入力層に入力します。

z^{(1)} = x_i

　第l-1層から第l層への伝播は以下のように行います。三層ニューラルネットワークでは１から２層、２から３層への伝播で行われます。
f(・)はベクトルの各要素に活性化関数を作用させます。

\bm{z}^{(l)} = f(\bm{u}^{(l)})
\bm{u}^{(l)} = W^{(l)}\bm{z}^{(l-1)}+\bm{b}^{(l)}

　伝播してきた出力を出力層から出力します。出力層を第L層とします。三層ニューラルネットワークではL=3となります。

\bm{y_i} = \bm{z}^{(L)}

となります。上記の入力から出力までを順伝播計算とします。

勾配降下法

係数の更新を行う方法として、勾配降下法を用います。
今回は確率的勾配降下法と呼ばれるものを利用します。

誤差関数

深層学習では出力が教師データに近づくように学習します。そこで教師データと出力の差を図る誤差関数を定義します。n番目の教師データと出力の誤差をE_nと表記し今回は二乗誤差として次のように計算します。

E_n = \frac{1}{2}\|\bm{y_n}-\bm{d_n}\|^2

確率的勾配降下法

上記で定義した誤差を用いて以下のように係数の更新を行います。

W^{(t+1)} = W^{(t)} - \epsilon \nabla E_n

\nabla E_nはE_nをWの各要素w_{ij}で微分した行列を意味することにします。
　上記の更新は各データの入力一度に対して一度行います。

\nabla E_nを計算する手法として次に誤差逆伝播法を紹介します。

誤差逆伝播法

w_{ij}^{(l)}での微分は以下のように変形できます。

ここで \frac{\partial E_n}{\partial u_i^{(l)}}を計算する際に以下のように計算します。今回は次のようになることの詳細は省略します。
\delta_i^{(l)} = \frac{\partial E_n}{\partial u_i^{(l)}}
\delta_i^{(l)} = \sum_{j=1}^n \delta_j^{l+1}(w_{jk}^{(l+1)}f'(u_k^{(l)}))

上記のように第l+1層の誤差が第l層に伝播しているので誤差逆伝播法と呼ばれます。

δの初期値

上記の誤差逆伝播法を行うとき出力層の\bm{\delta}^{(L)}を計算する必要があります。誤差を二乗誤差とする際には以下のように初期値を決定します。これも今回は証明は省略しますが、難しくないので是非計算してみてください。

\bm{\delta}^{(L)} = \bm{y} - \bm{d}

これで上記の初期値を利用して、誤差を伝播することによって各層の微分が計算できます。

ベクトル表記でのまとめ

上記で計算できますが、順伝播計算同様ベクトル表記を用いてまとめます。

\bm{\delta}^{(L)} = \bm{y} - \bm{d}
(\bm{\delta}^{(l)})^T = ((\bm{\delta}^{(l+1)})^TW) \circ f'(u^{(l)})^T
\nabla W_{ij}^{(l)} = \delta_i^{(l)}z_j^{(l-1)}

\circはベクトルの要素同士の積を意味します。
Tは転置を意味します。

まとめ

上記までの計算でニューラルネットワークの計算は一通りできます。
順伝播計算を行い、誤差逆伝播法で微分を計算し、係数を更新する。これを各データに対して行い学習します。データ数が少なく最適解にたどり着かない場合はその計算を何度か繰り返します。

参考文献

岡谷貴之(2015) ：『深層学習』, 講談社