前回まででニューラルネットワークの計算方法について説明しました。
いよいよ今回は、三層ニューラルネットワークをnumpyを用いて実装してみようと思います。

計算の詳細は前回ブログを参考にしてください。

三層ニューラルネットワークのフルスクラッチによる実装①
三層ニューラルネットワークのフルスクラッチによる実装②

補足

\bm{u}^{(l)} = W^{(l)}\bm{z}^{(l-1)}+\bm{b}^{(l)}

前回の解説では順伝播を上記のように計算しましたが、バイアスの計算を係数行列の０列目にバイアスを挿入し、ｚの０行目に１を挿入することで以下のように計算を行います。

具体的には以下の二式が等しいことを利用しています。

\left( \begin{array}{c}u_{1} \\ u_{2} \end{array}\right) = \left( \begin{array}{ccc}b_{1} w_{11} w_{12}\\ b_{2} w_{21} w_{22} \end{array}\right) \left( \begin{array}{c}1\\z_{1} \\ z_{2} \end{array}\right)

\left( \begin{array}{c}u_{1} \\ u_{2} \end{array}\right) = \left( \begin{array}{cc} w_{11} w_{12}\\ w_{21} w_{22} \end{array}\right) \left( \begin{array}{c}\\z_{1} \\ z_{2} \end{array}\right) + \left( \begin{array}{c}\\b_{1} \\ b_{2} \end{array}\right)

今回使用するライブラリは以下の通りです

import numpy as np
import matplotlib.pyplot as plt

活性化関数

　活性化関数としてシグモイド関数を利用します。ここではシグモイド関数とシグモイド関数の導関数を定義します。

def sigmoid(x):
    return 1/(1+np.exp(-x))
def del_sigmoid(x):
    return sigmoid(x)*(1-sigmoid(x))

順伝播計算

　次に入力ｘから出力z３までを計算する関数 ForwardPropagationを定義します。

ForwardPropagation(x,w2,w3)は入力ｘと係数行列を引数にとり、各種ｚ等を返します。

def ForwardPropagation(x,w2,w3):
    z1 = np.insert(np.array([x]).T,0,1,axis=0)
    u2 = np.dot(w2,z1)
    z2 = np.insert(sigmoid(u2),0,1,axis=0)
    u3 = np.dot(w3,z2)
    z3 = u3
    return dict(z1=z1,z2=z2,z3=z3,u2=u2)

　まずは引数について説明します。

x: リスト型またはベクトル　　　例　[1,2,3]
w2,w3: 配列 　　例　array([[1,2,3],[4,5,6]])

２行目ではリストで入力されるｘを列ベクトルの配列に変形しています。
また２行目、４行目では補足の通り、０行目に１を挿入しています。

誤差逆伝播法

　次に誤差逆伝播法を計算する関数BackPropagationを定義します。

BackPropagationは引数に教師ｙと各係数行列、ForwardPropagationの返値をとり、誤差関数の微分を返します。

def BackPropagation(y,w2,w3,z1,z2,z3,u2):
    d3 = (z3 - np.array([y]).T).T
    d2 = np.dot(d3,w3)[:,1:]*del_sigmoid(u2).T
    dw3 = d3.T*z2.T
    dw2 = d2.T*z1.T
    return dict(dw2=dw2,dw3=dw3)

ｙ:ｘ同様リストまたはベクトル
z１以降はForwardPropagationの出力

確率的勾配降下法

　上記で順伝播計算から誤差逆伝播法の計算を行う関数を定義しました。
次に誤差逆伝播法で計算された係数行列の勾配をりようして係数の更新を行う関数decentを定義します。

def decent(x,y,w2,w3,epsilon):
    f = ForwardPropagation(x,w2,w3)
    b = BackPropagation(y,w2,w3,f['z1'],f['z2'],f['z3'],f['u2'])
    w2 = w2 - epsilon*b['dw2']
    w3 = w3 - epsilon*b['dw3']
    return dict(w2=w2,w3=w3)

x,y,w2,w3は前と同様
epsilon: 学習率　係数をどの程度更新するかを決定します。

実際に学習を行う

以下では、係数の初期化から係数の学習を行う関数を定義します。

def train(X,Y,n2,epoch,epsilon):
    n1 = len(X[0])
    n3 = len(Y[0])
    w2 = np.random.normal(0,1,(n2,n1))
    w2 = np.insert(w2,0,0,axis=1)
    w3 = np.random.normal(0,1,(n3,n2))
    w3 = np.insert(w3,0,0,axis=1)
    for _ in range(epoch):
        for x,y in zip(X,Y):
            w = decent(x,y,w2,w3,epsilon)
            w2 = w['w2']
            w3 = w['w3']
    return dict(w2=w2,w3=w3)

X,Y : 教師、サンプルの入力（リスト）のリスト　例[[1,2,3],[2,3,4],...]
n2: 中間層のユニット数
epoch: サンプルに対しての学習を何回繰り返すかの回数
epsilon: 学習率

以上の関数にサンプルと教師データを入力すると、学習された係数行列を返してくれます。次にその係数を用いて予測を行う関数を定義します。

def predict(x,w2,w3):
    f = ForwardPropagation(x,w2,w3)
    return f['z3']

計算内容は学習された係数を利用して順伝播計算を行うだけです。

回帰をしてみる

　では実際にサンプルデータを発生させて回帰分析をしてみましょう。
サンプルは以下の分布より発生させます。

f(x) = (x-1)^2
X \sim normal(f(x),0.1)

20サンプルを[0,2]の範囲で発生させる

def f(x):
    return (x-1)**2
X = np.random.uniform(0,2,20)
Y = f(X) + np.random.normal(0,0.1,20)
plt.scatter(X,Y)
plt.show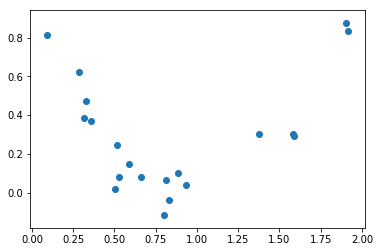

では、上記のサンプルに対して学習を行ってみます。
学習率は0.01、中間層ユニット数は5、学習は5000回行います。

X_train = np.array([X]).T
Y_train = np.array([Y]).T
w = train(X_train,Y_train,5,5000,0.01)
X_test = np.linspace(0,2,100)
Y_test = [predict(x,w['w2'],w['w3']) for x in X_test]
plt.plot(X_test,Y_test)
plt.scatter(X,Y)
plt.show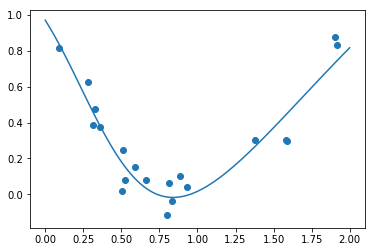

結果は上記のようになりました。うまく学習が行えているように見えます。最後に真の曲線f(x) = (x-1)^2 を描画し、比較してみます。
オレンジが真の曲線です。

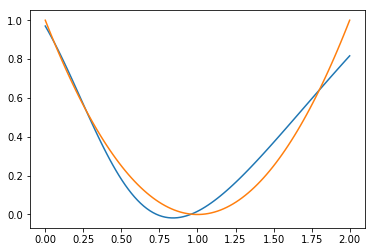
　右側はサンプル数が左側に比べ少ないため予測の精度が悪くなっています。
このように予測はサンプル数により変動します。

最後に

　三層ニューラルネットワークを実装して回帰に応用してみました。基本的な計算のみを実装しましたが、ミニバッチ学習や正則化など汎化性能を向上させる方法があるので調べて実装してみてください。余裕があったら更新してみようと思います。

参考文献

岡谷貴之(2015) ：『深層学習』, 講談社