【確率的プログラミング】Pyroを使ってMCMCや変分推論をしてみる

2020.06.25

【確率的プログラミング】Pyroを使ってMCMCや変分推論をしてみる

MCMC Pyro ベイズ統計変分推論

はじめに

Pyroを触ってみたので紹介します。今回はPyroを用いたMCMCと変分推論について扱います。

ベイズ推論については、

ベイズ推測の方法

変分推論については、

変分ベイズ入門

に紹介しているのでなんだそれはという人は確認してみてください。

MCMCについてもStanで実装したものが、

にあります。

Pyroとは

PyroはPythonで書かれた普遍的な確率的プログラミング言語で、バックエンドはPyTorchでサポートされています。
最新のディープラーニングとベイズモデリングの長所を統合した、柔軟で表現力豊かなディープな確率論的モデリングを行うことが出来ます。

【Pyro公式ページ】

ライブラリのインストールと読み込み

!pip install pyro-ppl

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.distributions.constraints as constraints
import pyro
import pyro.distributions as dist
from pyro.infer.mcmc import MCMC,NUTS #MCMCで利用します
from pyro.optim import Adam #変分推論に利用します
from pyro.infer import SVI, Trace_ELBO #変分推論に利用します
from pyro.infer import Predictive # 予測分布の計算に利用します

サンプリング

今回は次の関数を用います。
$y = \mathrm{Norm}(2*x + 5,1.)$

$x \in (-2,2)$ の範囲で20個サンプリングします。

x = np.random.uniform(-2,2,20)
y = 2*x + 5 + np.random.normal(0,1,20)
plt.scatter(x,y)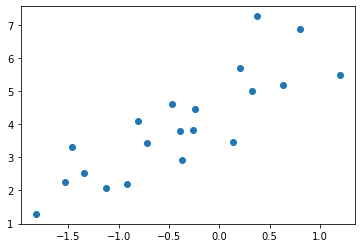

pytorchで利用するので上記のサンプルをtensorに変換します

x_tensor = torch.tensor(x)
y_tensor = torch.tensor(y)

モデル

変分推論、MCMCで以下のモデルを利用します。

def model(x,y):
    a = pyro.sample('a', dist.Normal(0., 5.))
    b = pyro.sample('b', dist.Normal(0.,5.))
    y = pyro.sample('y', dist.Normal(a*x + b, 1.), obs=y)
    return y

a、bはそれぞれパラメータで事前分布 $\mathrm{Norm}(0,5)$ に従います。
モデルは $\mathrm{Norm}(ax+b,1)$ とします。

yを観測した事を条件づける目的でobs = yを設定します。

MCMC

NUTSを用いたMCMCを行います。

nuts_kernel = NUTS(model, adapt_step_size=True)
mcmc_run = MCMC(nuts_kernel, num_samples=1000, warmup_steps=1000)
mcmc_run.run(x_tensor,y_tensor)

Sample: 100%|██████████| 2000/2000 [00:17, 117.44it/s, step size=7.27e-01, acc. prob=0.934]

上記のMCMCで得られたサンプルは次のように取得します。

posterior_a = mcmc_run.get_samples()['a']
posterior_b = mcmc_run.get_samples()['b']

次にこのサンプルを用いた予測分布の計算を行います。
こちらも関数一つで予測分布の計算が行えるので簡単です。

pred = Predictive(model,{'a':posterior_a,'b':posterior_b},return_sites=["y"])

上記で予測分布を作成し、実際に計算は次のように行います。

x_ = np.linspace(-2,2,100)
y_ = pred.get_samples(torch.tensor(x_),None)['y']

計算して得られた予測分布の平均と標準偏差を描画します

y_mean = y_.mean(0)
y_std = y_.std(0)
plt.figure(figsize=(10,5))
plt.plot(x_,y_mean)
plt.fill_between(x_,y_mean-y_std*2,y_mean+y_std*2,alpha=0.3)
plt.scatter(x,y)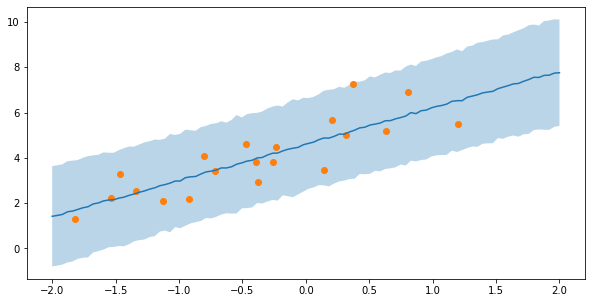

変分推論

近似事後分布を次のモデルとして用意します。

def guide(x,y):
    a_loc = pyro.param('a_loc',torch.tensor(0.))
    b_loc = pyro.param('b_loc',torch.tensor(0.))
    a_scale = pyro.param('a_scale',torch.tensor(1.),constraints.positive)
    b_scale = pyro.param('b_scale',torch.tensor(1.),constraints.positive)
    pyro.sample('a',dist.Normal(a_loc,a_scale))
    pyro.sample('b',dist.Normal(b_loc,b_scale))

変分パラメータとしてa_loc、b_loc、a_scale、b_scaleを用意し、
変分事後分布はa、bがそれぞれ独立に正規分布に従うとします。

変分推論は勾配を用いた勾配降下法により行います。
pytorchの実装のようにoptimizerを設定し最適化を行います。
目的関数はELBO(変分下界)になります

adam_params = {"lr": 0.001, "betas": (0.90, 0.999)}
optimizer = Adam(adam_params)
# setup the inference algorithm
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
n_steps = 1000
# do gradient steps
for step in range(n_steps):
    svi.step(x_tensor,y_tensor)

得られた変分パラメータを確認してみます。

for name in pyro.get_param_store():
    print(name + ':{}'.format(pyro.param(name)))

a_loc:1.593631386756897
b_loc:4.6159749031066895
a_scale:0.25455406308174133
b_scale:0.223267063498497

予測分布もMCMC同様Predictive関数を用いて計算できます

y_pred = Predictive(model=model,guide=guide,num_samples=1000,return_sites=["y"])

x_ = torch.tensor(np.linspace(-2,2,100))
y_ = y_pred.get_samples(x_,None)

y_mean = y_['y'].mean(0).detach()
y_std = y_['y'].std(0).detach()
plt.figure(figsize=(10,5))
plt.plot(x_,y_mean)
plt.fill_between(x_,y_mean-y_std*2,y_mean+y_std*2,alpha=0.3)
plt.scatter(x,y)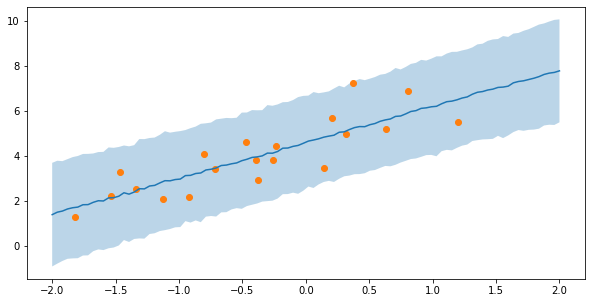

ほとんどMCMCに一致した結果が得られました。
近似事後分布に正規分布を設定しましたが、実際の事後分布も正規分布になるので
近似ではなく正しい事後分布を計算することができました。

一応MCMCのサンプルと近似事後分布を比較してみましょう。

# aについて
a = np.random.normal(pyro.param('a_loc').detach().numpy(),
                     pyro.param('a_scale').detach().numpy(),1000)
plt.hist(a,density=True,bins=50)
plt.hist(posterior_a,density=True,alpha=0.5,bins=50)
plt.show()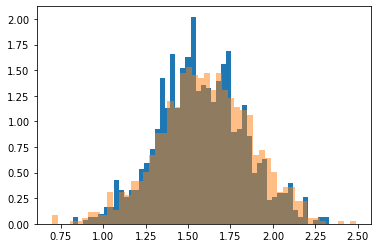

# bについて
b = np.random.normal(pyro.param('b_loc').detach().numpy(),
                     pyro.param('b_scale').detach().numpy(),1000)
plt.hist(b,density=True,bins=50)
plt.hist(posterior_b,density=True,alpha=0.5,bins=50)
plt.show()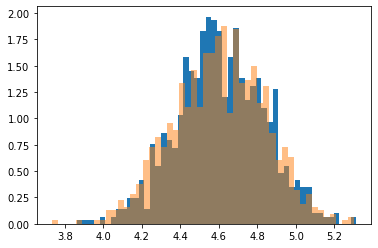

概ね一致していることが確認できます。

おまけ

pyro.clear_param_store()

上記を実行することで最適化されたパラメータをリセットすることができます。

今回は簡単な線形回帰を扱いましたが、深層学習モデルに対して近似事後分布を設定し変分推論を行うこともできます。

\ いいなと思ったらシェア /

ブログトップに戻る