目的
- VAEの構造を理解する(前回)
- VAEの学習方法を理解する。(今回)
前提知識
- 基本的なニューラルネットワーク
- 基本的な確率・統計の知識
VAEの学習方法
VAEの学習で問題となる点が存在します。
前編で目的関数を設計しましたので、あとは誤差逆伝播法を用いてパラメータに関する勾配計算が出来さえすればいいのですが、それが通常通りできません。
詳しく見ていきます。目的関数(ELBO)は以下の通りでした。
\mathcal{L}(\theta,\phi)=\mathbb{E}_{q_{\phi}(z|x)}[\log\ p_{\theta}(x|z)]-D_{KL}[q_{\phi}(z|x)||p(z)]
ここで、\theta・\phiはそれぞれデコーダー・エンコーダーのパラメータであり今回の学習対象です。
\theta,\phi の勾配は以下のように表せます。
\nabla_{\theta}\mathcal{L}(\theta,\phi)=\nabla_{\theta}\mathbb{E}_{q_{\phi}(z|x)}[\log p_{\theta}(x|z)] (第2項は\thetaに関して定数なので、勾配は 0 )
上の\nabla_{\theta}\mathcal{L}(\theta,\phi)では、勾配計算をしたいパラメータ\thetaは期待値の中にあるデコーダーp_{\theta}(x|z)のパラメータです。ここで、微分・積分の順序が可換であると考えると、
\nabla_{\theta}\mathcal{L}(\theta,\phi)=\nabla_{\theta}\mathbb{E}_{q_{\phi}(z|x)}[\log p_{\theta}(x|z)]=\mathbb{E}_{q_{\phi}(z|x)}[\nabla_{\theta}\log p_{\theta}(x|z)]ここで、一番右の形は以下のようにシンプルなモンテカルロ推定量(単純なサンプル平均)で推定できます。
\nabla_{\theta}\mathcal{L}(\theta,\phi)=\mathbb{E}_{q_{\phi}(z|x)}[\nabla_{\theta}\log p_{\theta}(x|z)]\approx \frac{1}{M}\sum_{i=1}^M \nabla_{\theta}\log p_{\theta}(x|z_i)次に\nabla_{\phi}\mathcal{L}(\theta,\phi)についてです。第2項については後程説明しますが、こちらはあまり問題にはなりません。問題となるのは第1項です。
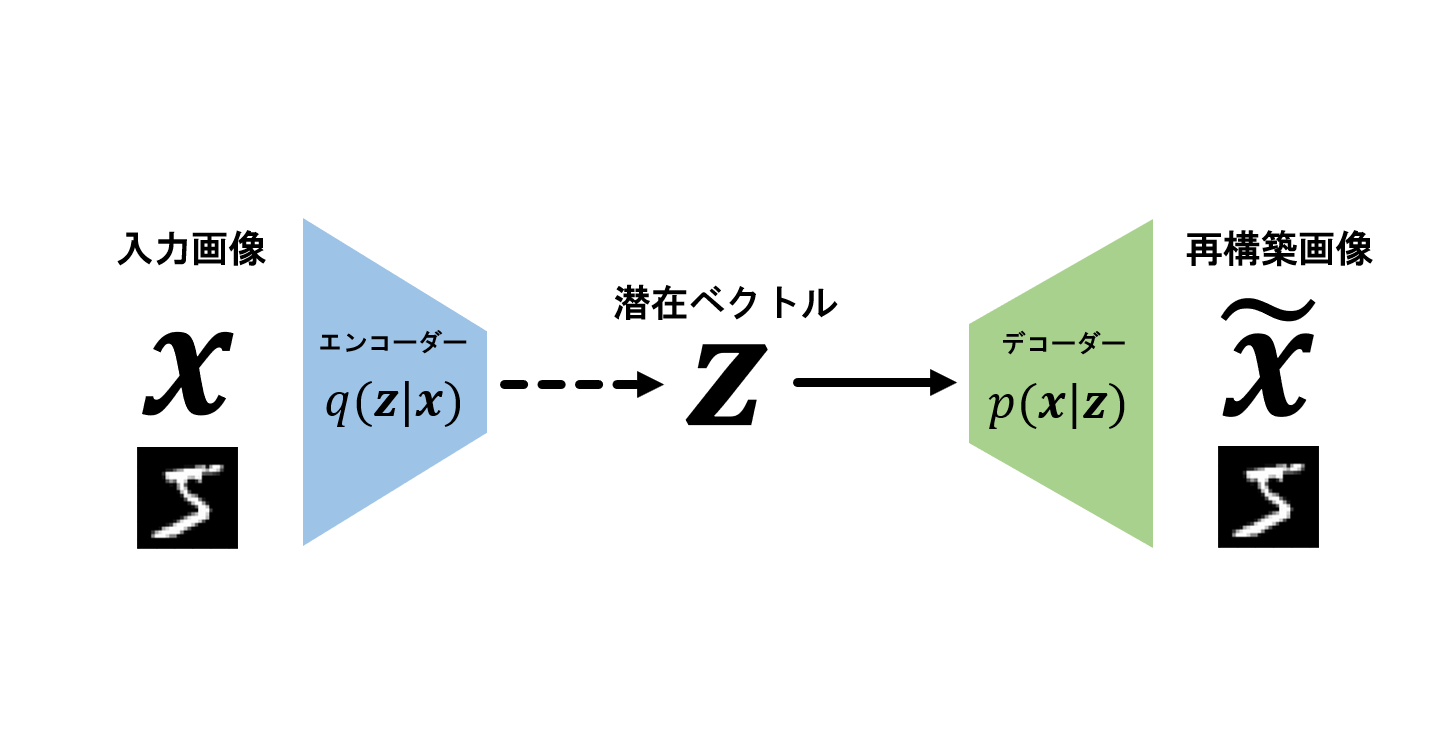
問題点を直感的に理解したいと思います。前回説明したようにVAEのアーキテクチャは以下のようになります。
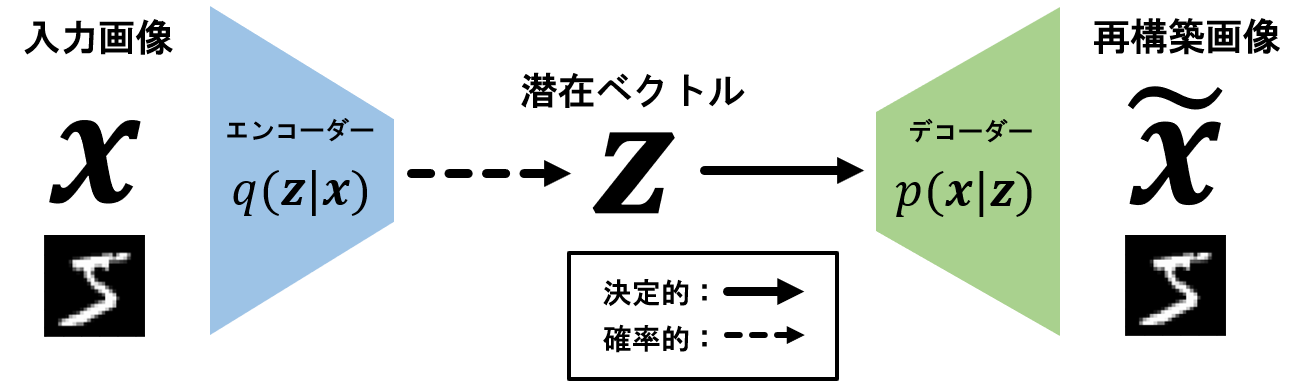
このモデル内の情報の流れは基本的には左から右です。
入力画像xをエンコーダーq_{\phi}(z|x)に入力
⇒ エンコーダーq_{\phi}(z|x)から潜在ベクトルzをサンプリング
⇒ 潜在ベクトルをデコーダーp_{\theta}(x|z)に入力
⇒ デコーダーからxをサンプリング
ここで2番目、4番目で「サンプリング」という言葉を使っていますが、実際には中でサンプリングしているわけではありません。イメージのために用いています。
このモデルの内部にはニューラルネットワークがあるため、エンコーダー・デコーダー内部のパラメータ\theta, \phiに関する勾配は誤差逆伝播法で求めます。通常通り、右から左に誤差を伝播していくことを考えると、通常ではありえない部分があります。それは、潜在ベクトルzがエンコーダーq_{\phi}(z|x)から「確率的に」サンプリングされている点です。ここが通常通りでなく、問題となる点です。確率的な潜在ベクトルからどのようにエンコーダーに誤差を伝播すればよいでしょうか?
その答えが「再パラメータ化」という手法です。この手法を理解するためにエンコーダーを詳しく見ていきます。ある画像x_iに対するエンコーダーは
q_{\phi}(z|x_i)=\mathcal{N}(z|\mathbf{\mu}_i,\mathbf{\sigma}^2_i \mathbf{I})ここで\mu_i, \sigma_iは、\mu_i=g_{\mu}(x;\phi)、\sigma_i = g_{\sigma}(x;\phi)のようにニューラルネットワークの出力です。先ほどの問題点は、サンプリングした潜在ベクトルzが確率的である点でした。
\frac{\partial z}{\partial\phi}=\frac{\partial z}{\partial \mu_i}\cdot \frac{\partial \mu_i}{\partial \phi}+\frac{\partial z}{\partial \sigma_i}\cdot \frac{\partial \sigma_i}{\partial \phi}上式の計算をしたいわけですが、zが確率的であるため、\phiに関して微分できない点(\mu_i,\sigma_iに関して微分できない点)が問題となります。要するに、\frac{\partial z}{\partial \mu_i},\frac{\partial z}{\partial \sigma_i}の部分が計算できません。
ここで、\epsilon \sim \mathcal{N}(0,\mathbf{I})という確率変数を導入して、\tilde{z}=\mu_i+\sigma^2_i\odot\epsilon としてみます。この確率変数\tilde{z}は q_{\phi}(z|x_i)=\mathcal{N}(z|\mathbf{\mu}_i,\mathbf{\sigma}^2_i \mathbf{I})に従う確率変数zと同等の確率変数であると言えます。(\odotはアダマール積・要素積で、ベクトルの要素ごとの積を計算しています)
しかも、これは\mu_i,\sigma_iに関して微分可能です。そのため通常通り誤差逆伝播法を用いて
\frac{\partial z}{\partial\phi}=\frac{\partial z}{\partial \mu_i}\cdot \frac{\partial \mu_i}{\partial \phi}+\frac{\partial z}{\partial \sigma_i}\cdot \frac{\partial \sigma_i}{\partial \phi}が計算でき、勾配法を用いた最適化が可能になります。このように新たな確率変数\epsilonを導入して、パラメータに関して微分可能な形にする手法を「再パラメータ化」と呼びます。
これにより、問題だった\nabla_{\theta}\mathcal{L}(\theta,\phi)の第一項が計算可能になります。続いて第二項についてです。エンコーダーは先ほどと同様 q_{\phi}(z|x_i)=\mathcal{N}(z|\mathbf{\mu}_i,\mathbf{\sigma}^2_i \mathbf{I})と仮定します。
\begin{aligned}-\nabla_{\phi}D_{KL}[q_{\phi}(z|x)||p(z)]&=\int q_{\phi}(z)(\log p_{\theta}(z)-\log q_{\phi}(z))dx\\&= \frac{1}{2}\sum_{j=1}^J(1+\log ((\sigma_j)^2))-(\mu_j)^2-(\sigma_j)^2)\end{aligned}こちらは明らかにエンコーダーq_{\phi}(z|x)のパラメータ\mu_j, \sigma_jについて微分可能ですので、特に問題になりません。
ここまでの説明から、目的関数に対するエンコーダー・デコーダーのパラメータ\theta,\phiの勾配計算の方法がわかったので、あとはSGDなりAdamなりを使って最適化すれば学習が可能です。
まとめ
今回はVAEの学習方法について、とりわけ内部に確率的な構造を持つ場合の勾配計算の方法について解説してきました。実は、今回説明したものに加えてエンコーダー・デコーダー内のネットワークの重みパラメータ\theta,\phiにも事前分布を仮定して、変分事後分布を計算することもできます。このようにフルにベイズで扱う方法はこの書籍にて解説されていますので、是非確認してみてください。次回はVAEの実装について触れていきたいと思います。


