
概要
この記事では, 「効果検証入門」のポイントをまとめ, 書籍内で行われている分析を掲載していきます.
(本記事は自分が勉強したことのまとめ的要素が強いので, 手元に書籍がある状態でお読みいただくことをオススメします)
尚, 分析コードについては著者が提供しているGitHubからダウンロードもできますので, 実際に手を動かしてみたい方は参考にしてください.
今回は第2章 回帰分析の前半(2.1~2.2)について取扱います.
第1章RCTについてはこちらをご確認ください.
2.1 回帰分析の導入(P40~P49)
単回帰分析
-
目的変数Yと変数Xの関係性を分析する
- Xが1単位増減したときにYがどう変化するかがわかる
-
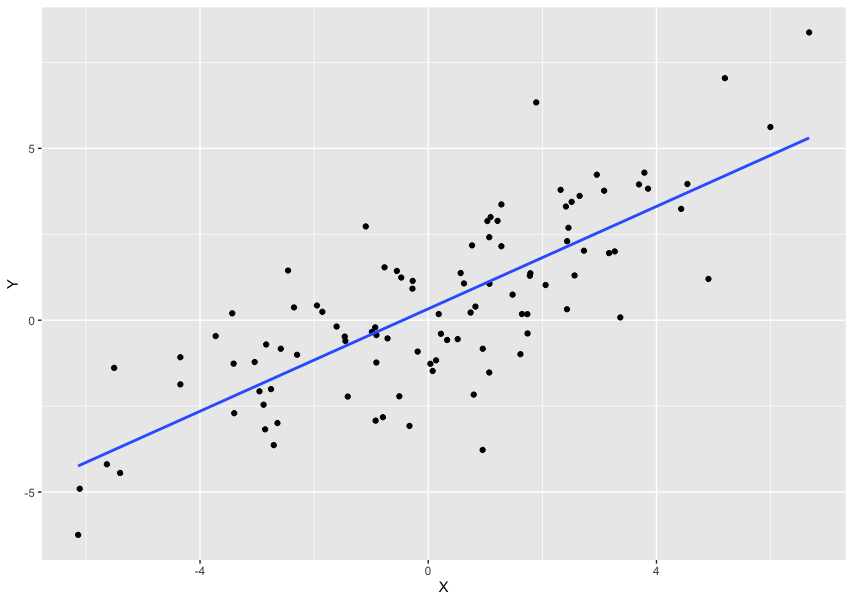
下の図は実際に単回帰分析を実行したときのイメージである

- ここでX=0のときのYの値が切片(\beta_0)となる
- この直線の傾きが\beta_1となる
- そして各点と直線との誤差はu_iであらわされる
-
よって, Y_iは
Y_i = \beta_0 + \beta_1X_i + u_i
となる - ここで\beta_0, \beta_1はパラメータである(分析で推定するもの)
- 手持ちのデータから得られた値は\hat{\beta_0}と\hat{\beta_1}とあらわす
- この回帰直線の誤差が小さくなれば各点の説明精度も高いことになるので, 最も小さくなるように線をひく→最小2乗法(OLS)
- 手元にあるデータから得られたパラメータ\hat{\beta}は, 母集団上で得られる\betaに対する推定値となる
-
ここで,
Y = E[Y|X] + u (E[Y|X]はYの条件付き期待値)
と分解できるので, Yに対する近似値を推定するだけでなく, Yの条件付き期待値の近似値を推定していることにもなる
効果分析のための単回帰分析
-
ここでは3種類の変数が登場する
- Y : 被説明変数
- Z : 介入変数
- X : 共変量
- 本著の例では, Yはメールマーケティングによる購買量, Zはメール配信をしたかどうか, Xは昨年の購買量や最後の購買日など分析者が選定するものである(基本Xは複数ある→重回帰分析)
- 重回帰分析においても単回帰分析と同様にパラメータの推定値と条件付き期待値が求まる
- モデル式にはXの2乗など柔軟に関数の形を導入できるが, これは分析者が適切に設定する必要がある
回帰分析による効果の推定
-
分析で知りたいのは介入があったかどうかで条件付き期待値に差があるのかどうかである. それぞれ
E[Y|X, Z = 1] = \beta_0 + \beta_1X + \beta_2X^2 + \beta_31
E[Y|X, Z = 0] = \beta_0 + \beta_1X + \beta_2X^2 + \beta_30
となるので, この差をみると,
E[Y|X, Z = 1] -E[Y|X, Z = 0] = \beta_3
である- つまりここでは介入変数である\beta_3に興味があるということになる
回帰分析における有意差検定
- 手に入れたデータからの推定値\hat{\beta_3}について有意差検定を行う. 結果の解釈については第1章と同様
Rによるメールメーケティングの分析(回帰編)
- 実際にバイアスのあるメールメーケティングデータに対して, 回帰分析を実行する
- 目的変数 : 購入額(spend)
- 介入変数 : メールの有無(treatment)
- 共変量 : 過去の購入額(history)
#まずは使用するパッケージの読み込み
library(tidyverse)
library(broom)#データについては以下のように加工
email_data <- read_csv("http://www.minethatdata.com/Kevin_Hillstrom_MineThatData_E-MailAnalytics_DataMiningChallenge_2008.03.20.csv")
male_df <- email_data %>%
#女性向けメール配信者を除外
filter(segment != "Womens E-Mail") %>%
#ダミー変数に変換
mutate(treatment = if_else(segment == "Mens E-Mail", 1, 0))
set.seed(1)
#条件に反応するサンプル量を半分にする
obs_rate_c <- 0.5
obs_rate_t <- 0.5
#バイアスデータの作成
biased_data <- male_df %>%
#コントロール群
#購買傾向が低いサンプルに1を与える
mutate(obs_rate_c = if_else((history > 300) | (recency < 6) |
(channel == "Multichannel"), obs_rate_c, 1),
#トリートメント群
#購買傾向が高いサンプルに1を与える
obs_rate_t = if_else((history > 300) | (recency < 6) |
(channel == "Multichannel"), 1, obs_rate_t),
#乱数発生
random_number = runif(n = NROW(male_df))) %>%
#メール未配信かつ発生させた乱数が0.5未満のコントロール群を半分抽出
filter((treatment == 0 & random_number < obs_rate_c)|
#メール配信かつ発生させた乱数が0.5未満のトリートメント群を半分抽出
(treatment == 1 & random_number < obs_rate_t))#回帰分析を実行(biased_dataは第1章で作成済)
biased_reg <- lm(spend ~ treatment + history, data = biased_data)
#分析結果の表示
summary(biased_reg)
- Coefficientsに注目すると, それぞれの\betaの値がEstimateから読み取れる
- また, p値についてはPr(>|t|)で確認できる
-
ここでtreatmentに注目すると推定値は0.9026109となっており, p値も十分に小さいことがわかるので「メール配信の効果はない」という帰無仮説は棄却できる
- よってメール配信をすると平均0.9程度売上があがる, と解釈できる
#coefficientsのみに注目したい場合broomパッケージで結果を表示する
biased_reg_coef <- tidy(biased_reg)
#データフレームで出力してくれる
biased_reg_coef
効果検証のための回帰分析で行わないこと
-
基本的にはtreatmentの結果以外には注目しない(その他のパラメータの値を改善するような努力をここではしないから)
- 有意差検定の結果もtreatment以外は解釈をしない
-
回帰分析の結果は予測器としても使えるが, 効果検証という観点ではspendの予測が目的ではない
- 予測式としては以下のようになる
spend = 0.324 + 0.903treatment + 0.001history
- 予測式としては以下のようになる
2.2 回帰分析におけるバイアス(P49~P66)
共変量の追加による効果への作用
-
共変量を増やすことで起きる結果を確認していく
- まず, RCTを行ったデータとバイアスのあるデータでメール配信の効果を確認
rct_reg <- lm(spend ~ treatment, data = male_df)
rct_reg_coef <- summary(rct_reg) %>%
tidy()
rct_reg_coef
nonrct_reg <- lm(spend ~ treatment, data = biased_data)
nonrct_reg_coef <- summary(nonrct_reg) %>%
tidy()
nonrct_reg_coef
-
それぞれのtreatmentの推定値が, 第1章で算出したメール配信有無での消費額平均の差と同様の結果である
- やはりセレクションバイアスによって過剰推定されていることがわかる
-
セレクションバイアスは人為的に発生しているおり, ここでは以下を共変量として追加する
- 最後の購入からの経過月数(recency)
- 昨年の購入額(history)
- 昨年どのチャネルから購入したか(channel)
nonrct_mreg <- lm(spend ~treatment + recency + history + channel,data = biased_data)
nonrct_mreg_coef <- summary(nonrct_mreg) %>%
tidy()
nonrct_mreg_coef
- treatmentの値は0.847と改善され, RCTにおける推定値0.770に近づいた
脱落変数バイアス(OVB)
- 追加すべき共変量 = 目的変数Yと介入変数Zに対して相関のある変数
- セレクションバイアスのあるモデルAとセレクションバイアスの影響を取り除いたモデルBを以下とする Y_i=\alpha_0+\alpha_1Z_i +u_i Y_i = \beta_0 + \beta_1Z_i + \beta_2X_i + e_i
- モデルAの誤差項u_i=\beta_2X+e_iとなっている
- ここでX_iはバイアスを取り除くのに必要な共変量である→脱落変数
-
モデルAにおける介入効果を示すパラメータ\alpha_1は,
\alpha_1= \beta_1+\gamma_1\beta_2-
この式からわかるように\alpha_1はモデルBにおける介入効果Zの推定値\beta_1と, 何かしらの値を取る\gamma_1\beta_2の和である
- \gamma_1\beta_2は脱落変数バイアス(OVB)と呼ばれている→必要な共変量を加えることでOVBの影響を取り除くことができる
- \beta_2はモデルBにおけるX_iとY_iとの相関にあたる
- \gamma_1はX_iに対して Z_i を回帰させてときの回帰係数である(Z_iとX_iの相関)
- よって, \gamma_1\beta_2はX_iとY_iとの相関に, X_iと Z_i の相関をかけたものである→推定値が歪められる
-
この式からわかるように\alpha_1はモデルBにおける介入効果Zの推定値\beta_1と, 何かしらの値を取る\gamma_1\beta_2の和である
-
ここで統計的に有意かどうかを考慮すると, 本来追加すべき共変量も取り除かれる可能性もあり, OVBを発生させてしまう
- よって, 介入変数以外のパラメータに関しては有意差検定の結果を気にする必要はない
RによるOVBの確認
-
昨年の購入額(history)が含まれているかどうかでモデル比較をする. historyは売上に対して強い相関をもつためOVBが発生する.
-
モデルA
spend_i = \alpha_0+\alpha_1treatment_i+\alpha_2recency_i+\alpha_3channel_i+e_i -
モデルB
spend_i = \beta_0+\beta_1treatment_i+\beta_2recency_i+\beta_3channel_i+\beta_4history_i+e_i -
また, OVBは以下のようになる
\alpha_1-\beta_1 =\gamma_1\beta_4 -
\gamma_1は回帰式であるモデルCであらわされる
history_i = \gamma_0 +\gamma_1treatmen_i+\gamma_2recency_i+\gamma_3channel_i+\epsilon_i
-
モデルA
-
上記モデルA~Cの回帰分析を実行していく
#それぞれのモデルをベクトルに格納 formula_vec <- c(spend ~ treatment + recency + channel, spend ~ treatment + recency + channel + history, history ~ treatment + channel + recency) #名前をつける #LETTERSで大文字アルファベットを指定できる #namesでデータに名前がつく names(formula_vec) <- paste("reg", LETTERS[1:3], sep = "_") #enframeでデータフレーム化できる models <- formula_vec %>% enframe(name = "model_index", value = "formula") #まとめて回帰分析を実行する #mapでそれを実行している #.xで使うベクトルやリストを指定, .fで関数や式を指定する df_models <- models %>% #回帰分析の部分 mutate(model = map(.x = formula, .f = lm, data = biased_data)) %>% #必要な部分だけ取り出す mutate(lm_result = map(.x = model, .f = tidy)) #モデルの結果を整える df_results <- df_models %>% #formulaを文字列に直す mutate(formula = as.character(formula)) %>% #selectで取り出す列を指定(このままだとネストデータ) select(formula, model_index, lm_result) %>% #分析しやすいようにunnestする(colsで取り出したい部分を選ぶ) #lm_resultに格納されているデータが展開される unnest(cols = c(lm_result)) df_results
-
ここで確認したいのは\alpha_1-\beta_1と\gamma_1\beta_4である.
-
まず, \alpha_1, \beta_1, \gamma_1を取り出す
#treatment行の中のestimateを取り出す treatment_coef <- df_results %>% filter(term == "treatment") %>% pull(estimate) treatment_coef
- 1つ目が\alpha_1, 2つ目が\beta_1, 3つ目が\gamma_1をあらわす
-
次に, \beta_4を取り出す
history_coef <- df_results %>% filter(model_index == "reg_B", term == "history") %>% pull(estimate) history_coef
-
OVBは\alpha_1-\beta_1, もしくは\gamma_1\beta_4なので,
#alpha-beta coef_gap = treatment_coef[1] - treatment_coef[2] #gamma*beta OVB <- treatment_coef[3] * history_coef coef_gap OVB

-
まず, \alpha_1, \beta_1, \gamma_1を取り出す
- よって共変量を追加したモデルと追加しなかったモデルとの推定される効果の差がOVBと一致することがわかる
OVBが与えてくれる情報
-
介入変数Zと目的変数Yの両方と関係性をもつような変数をモデルに含めるとバイアスを低減させることができるとわかった. このような変数を交絡因子と呼ぶ
- Yを予測するという観点ではYとの相関がないものを選ぶべきだが, OVBの値は0になるのでその変数をモデルに加えても効果の推定値は変わらない
- バイアスを減らすにはYとZどちらともある程度相関のある変数を加えることがポイント
- バイアスを発生させるような変数 (X_i)が手に入らなくても, その変数とY, Zの関係性が+, -どちらになるかを考えると推定が過剰か過少かが想定できる
Conditional Independence Assumption
-
効果検証において, モデルに含まれていない変数によるOVBが0になることが理想である
- これは介入Zがランダムに割り振られていることに等しい→CIA(Conditional Independence Assumption)
変数の選び方とモデルの評価
共変量の選択とCIA
-
分析者は以下のようなステップでモデルを作る
- どのように介入が割り当てられているのかを考える
- 介入の割り当てに関係のありそうな共変量を選択する
- 選択した共変量とYとの関係性を考え関数を決める
- このモデルがCIAを満たしている必要があるが, 2つの問題が考えられる
バイアスの評価ができないという問題
-
得られた効果の推定値がどの程度バイアスを持っているのかを評価できない
- OVBはモデル間のバイアスの変化を示しており, 残りのバイアスの大きさを示しているわけではない
必要な共変量がデータにはないという問題
- 手持ちのデータの中ではバイアスを最小にすることは可能でも, 他にバイアスを発生させる要因があると完全になくすことはできない
- ドメイン知識でバイアスを推察することもできるがこれは主観的評価が強まる
- これらの解決策としては操作変数法, 固定効果モデル, DIDなどが挙げられる
Sensitivity Analysis
-
手持ちのデータには含まれない変数がセレクションバイアスを引き起こしているかの評価方法→Sensitivity Analysis
- 分析者が重要だと認識している共変量以外の共変量をモデルから抜くことで, 効果の推定値が大きく変動するかどうかを確認する
- その結果推定値が大きく変化しないのであれば, ほかの変数による影響を受けにくいことを示唆する
Post treatment bias
-
OVBが0でない変数であればなんでも入れていいわけではない
-
ここではサイト来訪履歴(visit)を扱う
cor_visit_treatment <- lm(treatment ~ visit + channel + recency + history, data = biased_data) %>% tidy() cor_visit_treatment
- 結果から, 0.144程度相関があると考えられる
-
次に実際にモデルにvisitを追加してみる
bad_control_reg <- lm(spend ~ treatment + channel + recency + history + visit, data = biased_data) %>% tidy() bad_control_reg
- treatmentは0.294となり, 大きく減少した
- メール配信されたグループは購買意欲の高いユーザも購買意欲の弱いユーザもメールがあるからサイトに来訪している
- 一方メール配信されなかったグループは元々購買意欲の高いユーザだけサイトに来訪していることになる
- よって, サイト来訪有無で売上を比較するとメール配信されなかったグループの方が平均売上が高くなってしまう
-
ここではサイト来訪履歴(visit)を扱う
-
介入によって影響を受けた変数を入れることによって起きるバイアスをPost Treatment Biasという
- visitのように介入の後で決まるような値は分析から除外するべき
- なんらかの施策を評価する際は利用者や購入者だけでなく, 対象となるユーザ全体のデータを用意する必要がある
おわりに
同じ回帰分析でも目的によって結果の解釈や変数選択基準が異なってくることに新たな発見がありました.
次回は具体的な分析を行う第2章の後半(2.3~2.4)を取り上げたいと思います.
最後までお読みいただきありがとうございました.







![[Rによる演習付き]操作変数法を理解する](https://blog.deepblue-ts.co.jp/wp-content/uploads/writing-828911_1920.jpg)