非線形関数を用いたメディアミックスモデリング（MMM）

2020.09.17

非線形関数を用いたメディアミックスモデリング（MMM）

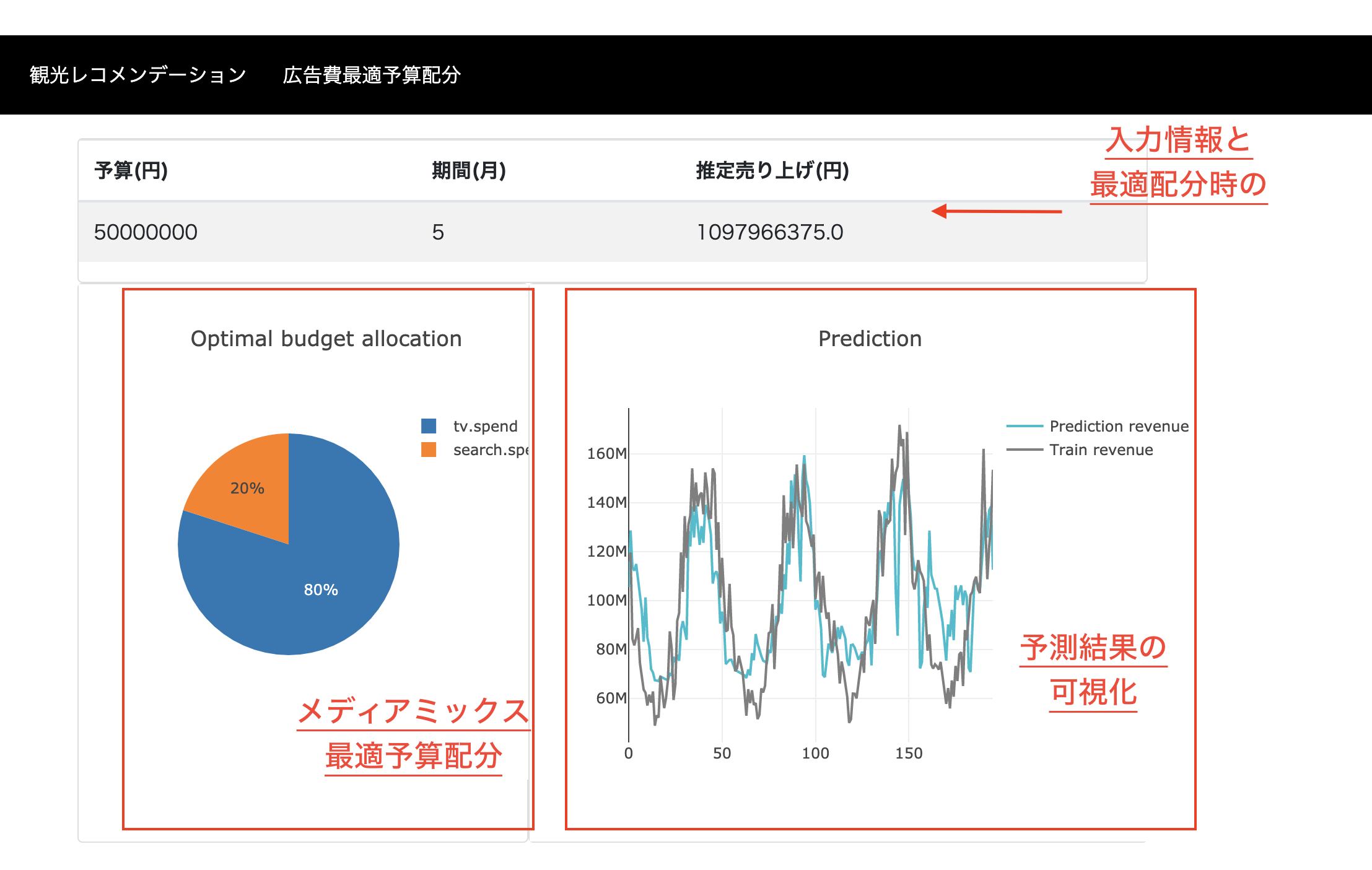
はじめに

今回はBayesian Methods for Media Mix Modeling with Carryover and Shape Effects
より形状効果、キャリーオーバー効果を考慮したメディアミックスモデル(MMM)について紹介します。
モデルについて紹介したあとpyroを用いてモデルの推測を行なってみます。

キャリーオーバー効果

${\rm adstock}(x_{t-L+1,m},...,x_{t,m};w_m,L) = \frac{\sum_{l=0}^{L-1}w_m(l)x_{t-l,m}}{\sum_{l=0}^{L-1}w_m(l)}$
$x_{t,m}$ のtは時刻、mはメディアを表します。 $w_m$ は残存効果となる重みを意味します。
論文中では単一のパラメータ $\alpha_m$ により
$w_m(l) = \alpha_m^l$
としています。

形状効果

形状効果を表す関数として、薬理学を起源に持つ次の関数が用いられています。
${\rm Hill}(x_{t,m};{\mathcal K}_m,{\mathcal S}_m) = \frac{1}{1 + (x_{t,m}/{\mathcal K}_m)^{-{\mathcal S}_m}}$
${\mathcal K}_m,{\mathcal S}_m$ の2つのパラメータにより関数の形状を調整します。

import numpy as np
import matplotlib.pyplot as plt

def Hill(x,K,S):
    return 1/(1 + (x/K)**(-S))

x = np.linspace(1e-5,1.5,100)
Ks = [0.5,0.5,1.5,1.5]
Ss = [1,2,2,1]
plt.figure(figsize=(10,7))
for S,K in zip(Ks,Ss):
     plt.plot(x,Hill(x,K,S),label = f'K:{K},S:{S}')
plt.legend()
plt.show()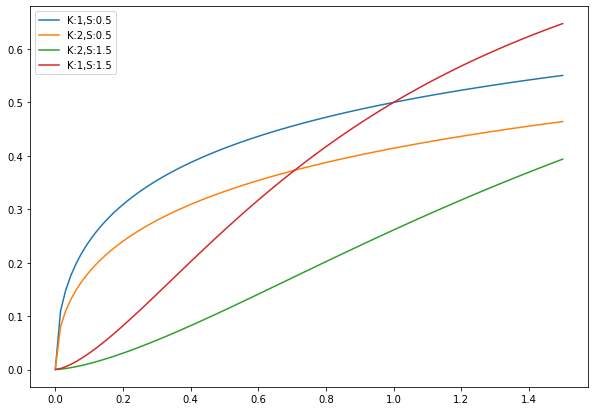

上記で紹介したHill関数は1に収束してしまいます。そこで、論文では新たに上限を意味するパラメータ $\beta_m$ を導入して $\beta_m {\rm Hill}(x_{t,m};{\mathcal K}_m,{\mathcal S}_m)$ を利用しています。
また、
$\beta_m {\rm Hill}(x_{t,m};{\mathcal K}_m,{\mathcal S}_m) = \beta_m - \frac{{\mathcal K}_m^{{\mathcal S}_m} \beta_m}{x_{t,m}^{{\mathcal S}_m}+{\mathcal K}_m^{{\mathcal S}_m}}$
が成り立ちます。

MMMモデル

adstock関数とHill関数を組み合わせて次のモデルを考えています。
$y_t = \tau + \sum_{m=1}^M \beta_m {\rm Hill}(x_{t,m}^{adstock};{\mathcal K}_m,{\mathcal S}_m) + \sum_{c=1}^C \gamma_cz_{t,c} + \epsilon_t$
$x_{t,m}^{adstock} = {\rm adstock}(x_{t-L+1,m},...,x_{t,m};w_m,L)$
$z_{t,c}$ は外生変数を意味しています。
$\tau$ は定数、 $\epsilon_t$ はホワイトノイズを表します。

モデル推定

論文ではSTANを用いたベイズ推測を行なっていますが、本ブログではpyroを用いた最尤推定によりパラメータ推定を行なってみます。
簡単のため外生変数はなしで行います。

データ生成

def Hill(x,K,S,beta):
    return beta - K**S*beta/(x**S + K**S)
def adstock(x,alpha):
    L = len(x)
    return sum(x*np.array([alpha**(L-l-1) for l in range(L)]))/sum(np.array([alpha**(L-l-1) for l in range(L)]))
true_param = [{'K':1,'S':0.5,'alpha':0.5,'beta':1},
              {'K':2,'S':1.5,'alpha':0.9,'beta':2}]
L = 13
x = np.random.uniform(0,2,(2,212))
x_adstock = np.array([[adstock(x_m[t-12:t+1],true_param[m]['alpha']) for t in range(12,112)] for m,x_m in enumerate(x)])
y = Hill(x_adstock[0],true_param[0]['K'],true_param[0]['S'],true_param[0]['beta']) + Hill(x_adstock[1],true_param[1]['K'],true_param[1]['S'],true_param[1]['beta'])
plt.figure(figsize=(10,5))
plt.plot(y)
plt.xlabel('time')
plt.ylabel('y')
plt.show()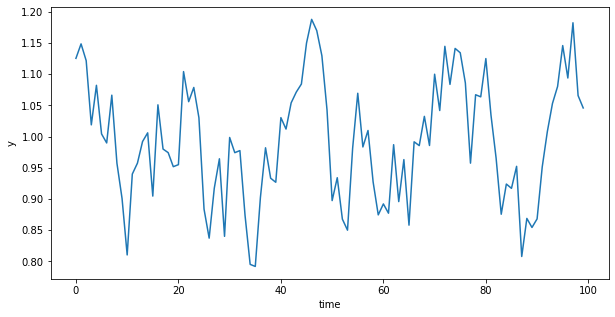

# pyroのインストール
! pip install pyro-ppl

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.distributions.constraints as constraints
import pyro
import pyro.distributions as dist
from pyro.infer.mcmc import MCMC,NUTS
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO
from pyro.infer import Predictive
from tqdm.notebook import tqdm

パラメータ推定

# モデル定義
def model(x,y):
    L = 13
    T = len(x[0])
    n = len(x) #メディア数
    var = pyro.sample('var',dist.InverseGamma(2,1))
    alpha = torch.ones((n,L,1))
    K = torch.ones((n,1))
    S = torch.ones((n,1))
    beta = torch.ones((n,1))
    for i in range(n):
        alpha_i = pyro.sample('alpha{}'.format(i),dist.Beta(3,3))
        for l in range(L):
            alpha[i,l,0] = alpha_i**l
        K[i,0] = pyro.sample('K{}'.format(i),dist.Beta(2,2))
        S[i,0] = pyro.sample('S{}'.format(i),dist.Gamma(3,1))
        beta[i,0] = pyro.sample('beta{}'.format(i),dist.Gamma(1,2))
    adstock = (x*alpha).sum(1)/alpha.sum(1)
    hill = beta - K**S*beta/(adstock**S + K**S)
    mu = hill.sum(0)
    y = pyro.sample('y',dist.Normal(mu,var**(0.5)),obs=y)
    return y

x_reshape = np.array([[x_m[t-12:t+1][::-1] for t in range(12,112)] for x_m in x]).transpose(0,2,1)

x_tensor = torch.tensor(x_reshape)
y_tensor = torch.tensor(y)
pyro.clear_param_store()
guide = pyro.infer.autoguide.guides.AutoDelta(model)
LR = 0.001
adam_params = {"lr": LR, "betas": (0.90, 0.999)}
optimizer = Adam(adam_params)
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
for step in tqdm(range(10000)):
    svi.step(x_tensor,y_tensor)

pred_param = [{'K':pyro.get_param_store()['AutoDelta.K0'].detach().numpy(),
              'S':pyro.get_param_store()['AutoDelta.S0'].detach().numpy(),
              'alpha':pyro.get_param_store()['AutoDelta.alpha0'].detach().numpy(),
              'beta':pyro.get_param_store()['AutoDelta.beta0'].detach().numpy()},
        {'K':pyro.get_param_store()['AutoDelta.K1'].detach().numpy(),
              'S':pyro.get_param_store()['AutoDelta.S1'].detach().numpy(),
             'alpha':pyro.get_param_store()['AutoDelta.alpha1'].detach().numpy(),
              'beta':pyro.get_param_store()['AutoDelta.beta1'].detach().numpy()}]

結果確認

true_param

[{'K': 1, 'S': 0.5, 'alpha': 0.5, 'beta': 1},
 {'K': 2, 'S': 1.5, 'alpha': 0.9, 'beta': 2}]

pred_param

[{'K': array(0.5604269, dtype=float32),
  'S': array(1.9417641, dtype=float32),
  'alpha': array(0.49627396, dtype=float32),
  'beta': array(0.29030246, dtype=float32)},
 {'K': array(0.64207244, dtype=float32),
  'S': array(2.0859094, dtype=float32),
  'alpha': array(0.87873966, dtype=float32),
  'beta': array(1.1397039, dtype=float32)}]

x_adstock_pred = np.array([[adstock(x_m[t-12:t+1],pred_param[m]['alpha']) for t in range(12,212)] for m,x_m in enumerate(x)])
y_pred = Hill(x_adstock_pred[0],pred_param[0]['K'],pred_param[0]['S'],pred_param[0]['beta']) + Hill(x_adstock_pred[1],pred_param[1]['K'],pred_param[1]['S'],pred_param[1]['beta'])
x_adstock = np.array([[adstock(x_m[t-12:t+1],true_param[m]['alpha']) for t in range(12,212)] for m,x_m in enumerate(x)])
y = Hill(x_adstock[0],true_param[0]['K'],true_param[0]['S'],true_param[0]['beta']) + Hill(x_adstock[1],true_param[1]['K'],true_param[1]['S'],true_param[1]['beta'])
plt.figure(figsize=(10,5))
plt.plot(y_pred,label = 'pred')
plt.plot(y,label = 'true')
plt.xlabel('time')
plt.ylabel('y')
plt.legend()
plt.show()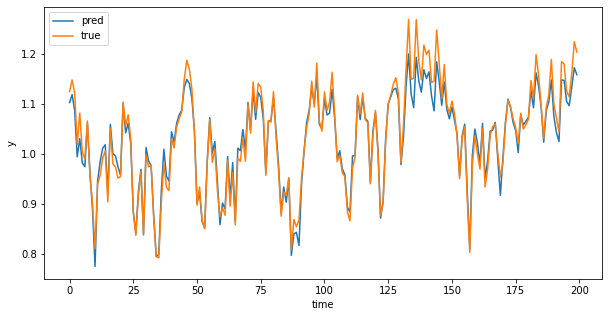

パラメータは一致していませんが、推測は一致していることが確認できます。
時刻100以降は学習データに加えていませんが適切に推測できていることも確認できます。

最後に

今回はHill関数を用いたMMMモデルを紹介しました。メディアの相互効果など、モデルは複雑になりますが加えて考慮できる点はありそうです。

\ いいなと思ったらシェア /

ブログトップに戻る