対象読者
時系列分析とは?
時系列分析とは、時間の経過に沿って記録されたデータ(時系列データ)を分析することです。時系列分析を行うことで過去の傾向や周期性を元に未来の変動を予測することができます。
時系列分析が他の統計分析と異なるのが各時点のデータとの関連に着目して分析する点です。時系列に沿っているデータであるため、各時点のデータ同士は関連しており、その関連のパターンをうまくモデルに取り込むことが重要になります。そのため自己相関や偏自己相関を頻繁に分析することになります。
例えば作成したモデルの精度を検定する際にはモデルの残差に有意な自己相関が残っていないかを調べます。もし、有意な自己相関が残ってしまうとまだモデルに取り込めていないデータの季節性やトレンドがあるということになります。
実際に分析する
今回はアサヒビールのHPに掲載されている月次販売データから、ビールの販売量(千箱)を取得し、エクセルで日付ラベルをつけてデータを成形しました。
使用したデータはこちらからダウンロードできます。
分析にはPythonのstatsmodelsという統計分析のためのパッケージを使用します。
データがダウンロードできたら早速分析に移っていきましょう。
その際に「date」というカラムがあるのでそのカラムをdatetime型にしてインデックスに指定します。また、後程モデルを作成する際にint型が含まれているとエラーが起きてしまうのでdtypeをfloat型に指定します。
今回は単変量の分析になるのでデータフレームを使う必要はないため、Seriesだけを取り出します。
# ライブラリ読み込み
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import statsmodels.api as sm# データ読み込み
row_data = pd.read_csv("beer_data.csv", index_col='date', parse_dates=True, dtype='float')
data = row_data["shipments"]
data.head()
次にデータを可視化します。
# データを可視化する
fig = plt.figure(figsize=(10,5))
plt.plot(data)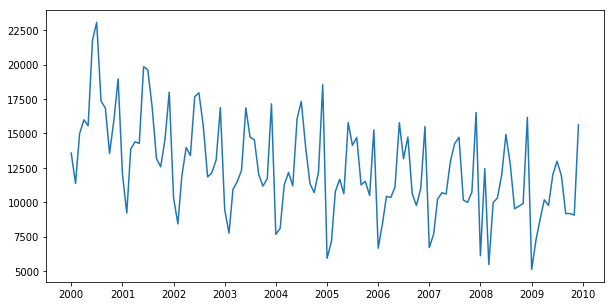
原系列だけではデータの特徴をつかみにくいので、自己相関と偏自己相関のコレログラムも図示します。
# 自己相関のコレログラム
fig = plt.figure(figsize=(18,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data, lags=40, ax=ax1)
# 偏自己相関のコレログラム
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data, lags=40, ax=ax2)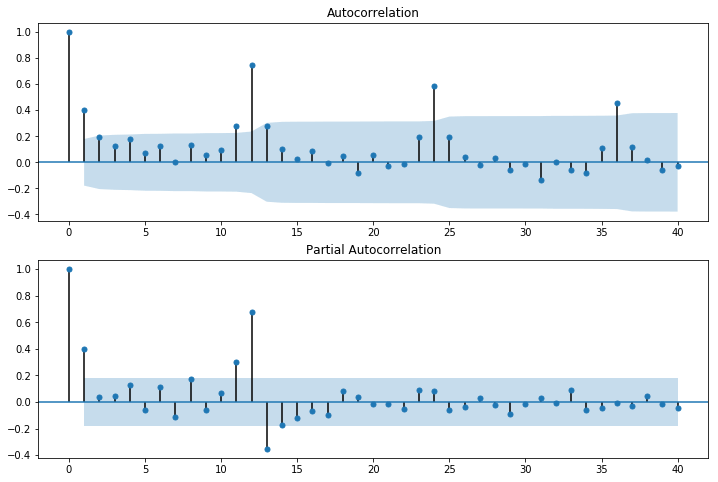
自己相関のコレログラムをみると、12か月周期で相関があることがわかります。
次に、トレンドを把握するために、データをトレンドと季節成分に分解します。ここではstatsmodelsのseasonal_decomposeという関数を使います。この関数はfreqで周期を指定する必要がありますが、今回は月次データなので12か月周期に指定します。
# データをトレンドと季節成分に分解
seasonal_decompose_res = sm.tsa.seasonal_decompose(data.values, freq=12)
seasonal_decompose_res.plot()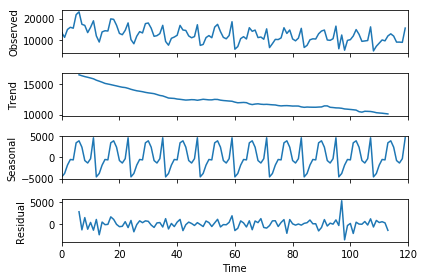
図示されたtrendを見ると、原系列データのグラフと比べるとグラフがなめらになっていて、全体の傾向がわかりやすくなりました。このデータには右肩下がりのトレンドがあることがわかります。
ここまででデータの大まかな特徴がわかったので、次はモデルを作成するためにデータの定常性について検定を行います。
今回はADF検定を用います。
# トレンド項あり(2次まで)、定数項あり
ctt = sm.tsa.stattools.adfuller(data, regression="ctt")
# トレンド項あり(1次まで)、定数項あり
ct = sm.tsa.stattools.adfuller(data, regression="ct")
# トレンド項なし、定数項あり
c = sm.tsa.stattools.adfuller(data, regression="c")
# トレンド項なし、定数項なし
nc = sm.tsa.stattools.adfuller(data, regression="nc")
print("ctt:")
print(ctt)
print("---------------------------------------------------------------------------------------------------------------")
print("ct:")
print(ct)
print("---------------------------------------------------------------------------------------------------------------")
print("c:")
print(c)
print("---------------------------------------------------------------------------------------------------------------")
print("nc:")
print(nc)
print("---------------------------------------------------------------------------------------------------------------")ctt:
(-1.1296428241080645, 0.9809873485998419, 13, 106, {‘1%’: -4.48392099206056, ‘5%’: -3.8893150700242485, ‘10%’: -3.5883089687795966}, 1825.1879732226598)
—————————————————————————————————————
ct:
(-3.4123499516224856, 0.04975962873572997, 13, 106, {‘1%’: -4.0468193247781725, ‘5%’: -3.452751165593073, ‘10%’: -3.151810567112449}, 1824.7894591881814)
—————————————————————————————————————
c:
(-4.133913657275536, 0.0008507909265923256, 13, 106, {‘1%’: -3.4936021509366793, ‘5%’: -2.8892174239808703, ‘10%’: -2.58153320754717}, 1827.8871241502568)
—————————————————————————————————————
nc:
(-5.763813542860867, 2.9719440529879815e-08, 12, 107, {‘1%’: -2.5869521233295485, ‘5%’: -1.9437787052372857, ‘10%’: -1.6145541037008495}, 1836.6902003349646)
—————————————————————————————————————
出力結果の2番目の値がp値です。ADF検定ではでデータが単位根過程であることが帰無仮説になっていているので、棄却することができればデータが単位根過程でない、つまり定常であると判断できます。
今回の検定ではトレンド項を2次までにした場合が棄却できませんでした。そのため、確実にデータが定常だとは言えないので、次回はデータを非定常なものとして扱いながらモデルを推定していきたいと思います。


