
PyStanでベイズ推論+MCMC法によるデータ分析①(Stanの基本)
はじめに
こんにちはdeepblueでインターン生として働いている東です。
MCMCについての学習を最近始めました。この記事を連載1記事目とし少しでもわかりやすい説明ができたらと思ってます。
この連載の目的としてはPyStanについての書籍や記事がRに比べて少ないと感じたため、これからPyStanに入門しようとしている人の手助けになれたらと思います。
pythonのStanに関するライブラリとしてはPyStan、PyMC3、Edwardあたりが有名だと思いますが今回はPyStanのみを扱います。
またベイズ統計MCMCについての原理や理論にはこの記事ではあえて扱わず、実装することで統計モデリングの世界に慣れていくというスタンスでやります。
それではよろしくお願いいたします。
PyStanでベイズ推論+MCMC法によるデータ分析②(MCMCの結果と評価)
PyStanでベイズ推論+MCMC法によるデータ分析③(単回帰モデル)
使用参考書籍 Rとstanではじめるベイズ統計モデリングによるデータ分析入門
初学者向けの入門書でありベイズ統計モデリングMCMCをRstanで基礎的扱い方から応用的な状態空間モデルまで幅広く解説しているこの本を選びました。
本記事で使用するデータセット下記のリンクからダウンロードしました。
https://github.com/logics-of-blue/book-r-stan-bayesian-model-intro
この記事について
第2部4章から実装していきます。
データの読み込み、Stanの使い方、事後分布に従う乱数の生成までが本記事の内容となっています。
ビールの売り上げデータが正規分布に従うと仮定してモデル化を進めます。ビールの売り上げsalesを平均\mu 分散を\sigma^2としたとき以下のように計算できます。
データの準備と可視化
第2部4章から実装していきます。
pythonライブラリーの読み込みと使用データの簡単な可視化を行います。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pystan
import seaborn as sns; sns.set() #seaborn見た目がきれい
stan=path+'2-4-1-calc-mean-variance.stan' #データの読み込み
beer=pd.read_csv(path+'2-4-1-beer-sales-1.csv') #データの読み込み
print(beer.describe()) #データの概要を出力
plt.hist(beer.sales,color='#111155') #ヒストグラムで可視化
plt.xlabel('temperature',fontsize=18)
plt.ylabel('sales',fontsize=18)
plt.show()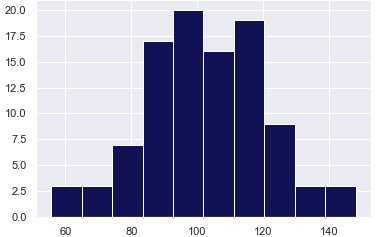
sales count 100.000000
mean 102.177600
std 17.963943
min 55.710000
25% 90.117500
50% 102.280000
75% 113.827500
max 148.030000
Stanファイルの書き方
次はStanファイルについて見ていきます。慣れないデータ型ですが理解して使うようにしましょう。
data {
int N; // サンプルサイズ
vector[N] sales; // データ
}
parameters {
real mu; // 平均
real sigma; // 標準偏差
}
model {
// 平均mu、標準偏差sigmaの正規分布に従ってデータが得られたと仮定
for (i in 1:N) {
sales[i] ~ normal(mu, sigma);
}
}- dataブロック
サンプルサイズと売り上げデータを指定してあります。サンプルサイズは整数なのでint型で宣言されています。売り上げデータはベクトルとしてvector[N]と宣言してあります。ベクトル型の他には行列型とアレイ型があります。 - parameters ブロック
推定したいパラメータを定義します。今回は平均と標準偏差を推定します。Stanでは分散ではなく標準偏差をパラメータとして与えます。変数の型がrealとする実数値型と宣言することができます。 - model ブロック
売り上げデータは平均muと標準偏差sigmaの正規分布に従うと指定します。チルダ(~)の記号で正規分布に従うということを表現できます。
Stan実行と乱数の出力
pythonのデータフレームからMCMCを実行するためにはデータを辞書型に変更する必要があるそうです。簡単にStanパラメータの説明をします。
- iter: 繰り返し回数
2000がデフォルトなのでそれくらいがいいと思います。
収束が悪いとき大きいiterを設定しましょう。 - chains : 乱数生成のセットの個数
4が設定されることが多いようです。 - thin: 間引き数
thin=3と設定されたときは3つの乱数のうち1つを採用するというように使われます。乱数の自己相関を緩和できるようです。 - warmup: バーンイン期間の設定
最初の一部分の乱数は切り捨てるようにします。初めは収束していないためです。
N=len(beer)
data=beer.sales.values
input_data = {'N': N, 'sales':data}
fit = pystan.stan(
file=stan #Stanファイル
,data=input_data #対象データ
,iter=2000 #乱数生成の繰り返し回数
,chains=4 #チェーン数
,thin=1 #間引き数
,warmup=1000 #バーンイン期間
,seed=1 #乱数の種
)
mcmc_sample = fit.extract(permuted=True)
print(mcmc_sample)OrderedDict
([('mu', array([103.18037416, 104.6213833 , 101.30711915, ..., 104.5467978 , 101.75741894, 99.57048929])),
('sigma', array([19.63982944, 18.38568699, 19.37303907, ..., 20.56768437, 18.00689899, 16.15128188])),
('lp__', array([-336.32140706, -336.3841442 , -336.08641784, ..., -337.77233107, -335.47607947, -337.95500281]))])
乱数を可視化し収束の確認をする
plt.style.use('default')
warmup = fit.extract(permuted=False, inc_warmup=True) #収束する前のデータもとる
pname = fit.sim['fnames_oi'] #パラメータ名の取得
iter_time = np.arange(0, warmup.shape[0]) #繰り返し回数
fig,axes = plt.subplots(nrows=2, ncols=1, figsize=(15,10))
for i in range(2):
for j in range(4): #プロット開始
axes[i].plot(iter_time, warmup[iter_time, j, i], linewidth=2,label="chain:"+str(j))
axes[i].set_title(para[i])
axes[i].legend()
axes[i].grid()
fig.show()
MCMCサンプルの初期の値は大きく変化しており安定していないことがよくわかります。このサンプルでは100回繰り返す前あたりには\muも\sigma^2もある値に収束していることがわかります。
pythonだと可視化するのにコードを数行かかないといけませんが、Rならもっと簡単にかけるようです。
まとめ
いかがだったでしょうか?まだまだ統計と言ったらRですがこれを読んでpythonで統計モデリングしたいと思うかたが増えればと思ってます。
次回はMCMCの評価や事後分布の可視化について触れていきます。
良かったら読んでみてください。


