
はじめに
前回のブログでは、統計的因果探索にLLMを組み合わせることで、専門家の知識なしに自動的にかつ自然な因果探索を行える手法、SCP(Statistical Causal Prompting) をご紹介しました。そして簡単に実装を行った結果を出力されたパス図と一緒に考察しました。
まだご覧になっていない方は前回のブログをこちらからご参照ください。
前回の実装時、マーケティングデータに応用することを目的としつつも、因果探索のアルゴリズムが時系列データに対応していなかった点により改善が必要であることがわかりました。
LiNGAMファミリーの中にはVAR-LiNGAMという時系列データに対応した因果探索アルゴリズムが存在しますが、このアルゴリズムにはSCPフレームワークの肝となる事前知識(prior knowledge)を直接は組み込めない難点があります。
そのため今回は、前回同様DirectLiNGAMを用いつつ、prior knowledgeの制約で擬似的にVARモデルを組み込むことにより実装を行います。
本記事では、SCPフレームワークの簡単なおさらいをした後、DirectLiNGAMでVARモデルを表現した方法を解説し、その後、マーケティング関連の売上・ウェブサイトデータに適用してみます。
SCPフレームワークのおさらい
SCP(Statistical Causal Prompting)は、統計的因果探索(SCD)の結果を大規模言語モデル(LLM)に渡し、その知識によって因果関係の妥当性を補強し、再度SCDに反映させるフレームワークです。
SCPは、統計的因果探索だけでは不自然な因果関係が生まれてしまうという問題に対して「LLMによるドメイン知識の補完」を導入し、より自然で解釈可能な因果構造を得ることを目指しています。
Takayama, et. al. (2024). [^1] の論文では、以下のようなプロセスが解説されています。
SCPのプロセス
- 統計的因果探索(SCD)を実行する
- LLMに対して「SCDで得られた因果関係」を提示し、ドメイン知識的に適切かを問う
- 生成された説明を踏まえて、再度LLMに因果関係の存在が妥当である確率を問う
- 得られた確率から、事前に設定した閾値によってエッジの存在を強制、不明、禁止に振り分け、prior knowledgeという制約(隣接行列)を作る
- 必要な場合はprior knowledge内のエッジの循環を削除する
- prior knowledgeを組み込んで再度SCDを行う
このようなプロセスにより、統計的にもドメイン知識的にも妥当な因果探索を行うことができるのがSCPフレームワークの強みです。
図1:統計的因果プロンプティング(SCP)の全体的枠組み[^1]

DirectLiNGAMでVARモデルを表現する方法
前回のブログでは、SCDのアルゴリズムにDirectLiNGAMを用いました。DirectLiNGAMにはモデルの引数にprior_knowledgeが設定されているため実装がしやすく、何よりもこのSCPフレームワークはLiNGAMの開発を率いる清水教授らの研究であり親和性が高いからです。ただ、SCPフレームワークの論文内では時系列データへの応用は記述されていなかったため、前回はまずは時系列効果を考慮せずに実装しました。
SCDの時系列データへの応用としては、すでにVAR-LiNGAMというモデルが存在していますが、SCPで必要となるprior_knowledge引数が設定されていないため、SCPフレームワークをそのまま応用することができない問題があります。(後にlingam_model引数によってprior_knowledgeを設定したDirectLiNGAMを引き継ぐことができると分かったため、その方法は次回以降のブログにてご紹介します。)
よって今回はDirectLiNGAMのみでどうにかVARモデルを表現できないかを考えました。
具体的には、元データ(現在項)を1期ずらした列(過去項)を追加し、過去項への全てのエッジの出現を禁止したprior knowledge制約を最初から用いることで現在項と過去項の関係を表現します。つまり、現在→過去、過去→過去のエッジを最初から出現させないように制約することで、現在→現在と過去→現在のパターンのみを出現させます。こうすることで、現在→現在のエッジでは即時効果、過去→現在のエッジでは遅延効果を表現することができるようになります。
図2:即時効果・遅延効果を表現するprior knowledge制約の考え方
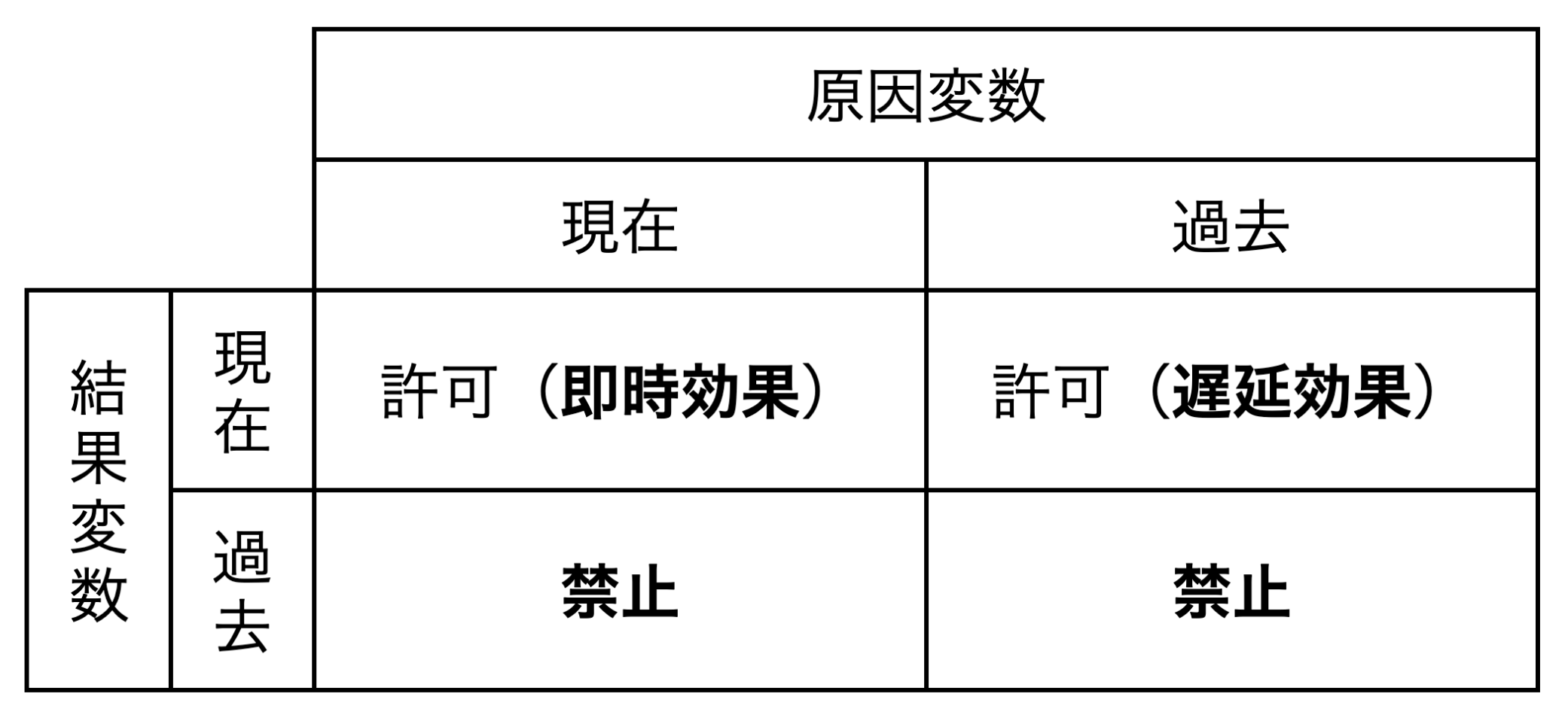
留意するべき問題点として、過去の項をいくつにするかは事前に決めておかなければならないこと、また複数項追加するにはモデルの改良が複雑になることがあります。扱う時系列データによっては、1期前よりも2期前、3期前の原因が現在に影響を及ぼしていることもあり、1期前のみを追加することが正しいとは言えないのです。特に日次データなどではそのような問題が起こりうると考えられます。
例として、あるレストランの広告を見た時、その日や次の日などすぐに来店する人もいれば、2日3日経ってから来店する人もいます。このように日次データを扱っている場合は、過去の項が1期分だけでは足りないこともあり、注意が必要です。
今回扱うデータは月次データのため、数日のずれは現在項の即時効果に吸収されており、過去項を1期分だけ追加することにはある程度合理性があると思います。よってこの方法にて進めます。
(将来的にはこのような属人的判断を全てLLMに行なってほしいと思います。)
ダミーデータで実験
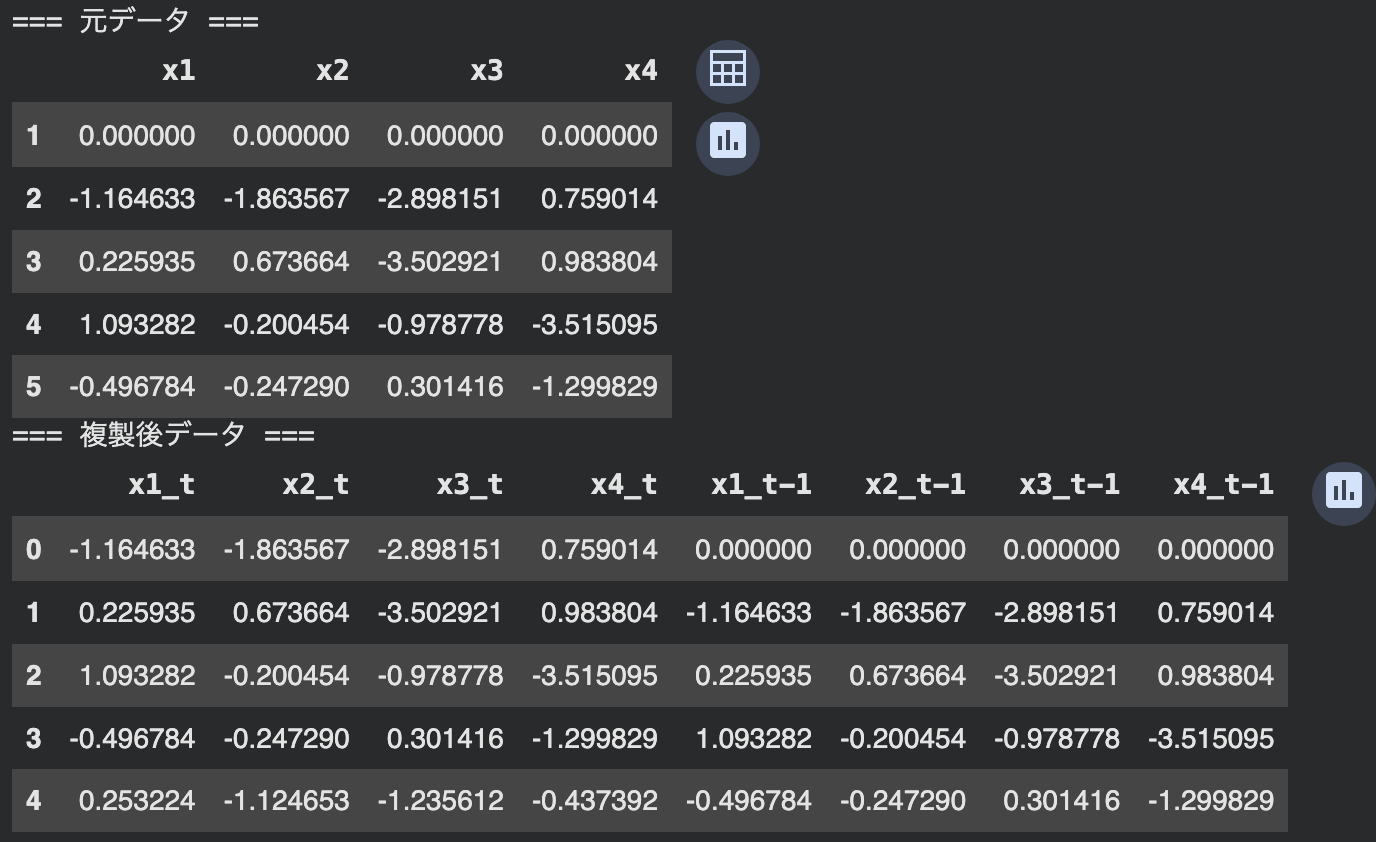
以下のように4行×20列のダミーデータを準備します。(画像には最初の5列のみを表示しています)。DirectLiNGAMを用いるため、モデルに学習させる前に過去項を複製して、変数の名前にtまたはt-1を追加し、現在項か過去項かをわかるようにしています。LiNGAMはデータの非ガウス性を仮定しているため、ここではラプラス分布に従うランダムなデータを作成しました。
図3:使用するダミーデータ
そして1回目のSCD(DirectLiNGAM)を行う前に、以下のようなprior knowledge制約(隣接行列)を作成します。
図4:隣接行列で表したprior knowledge制約

ここで0は禁止を、-1は不明を表しています。0が入っている部分は対角線と下半分です。対角線は、各変数がそれ自身への因果効果を持たないことを表し、下半分の0は過去項に対してどの変数も因果効果を与えてはいけないことを表します。エッジを強制させる場合は1を入れますが、ここでは制約を設けないので1はありません。
このようなprior knowledgeを持たせてDirectLiNGAMを行うことを擬似VAR-LiNGAMと呼ぶことにします。ダミーデータに対して擬似VAR-LiNGAMを行った結果が以下のようになります。
図5:擬似VAR-LiNGAMの結果
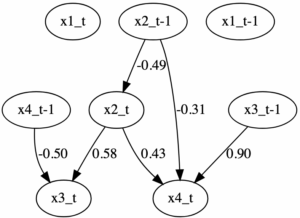
即時効果はt期の変数間で表され、遅延効果はt-1期の変数からt期への変数のエッジで表されています。
ちなみに元データに対してラグ1でVAR-LiNGAMを行った時は以下のようになります。
図6:VAR-LiNGAMの結果
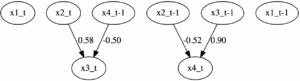
図5とは少し違いますが、よく見ると図5で出現している x2_t-1 → x2_t → x4_t のパスが図6の方ではが直接 x2_t-1 → x4_t となっているだけだと分かります。
図5のパス図における x2_t-1 から x4_t への因果効果を実際に計算してみると、
-0.49 * 0.43 -0.31 = -0.5207
となり、図6で x2_t-1 → x4_t の係数が -0.52 であることと一致します。
変数 x2_t-1 が結果的に影響を与える変数が x4_t のみであることを正確に描き分けているという点においてVAR-LiNGAMの方が優れてはいますが、DirectLiNGAMでもVARモデルを表現できると分かります。
この方法の利点は、SCDのアルゴリズムがDirectLiNGAMであることで、出現したすべてのパス(即時効果・遅延効果含む)についてLLMに妥当性を考えさせ、ドメイン知識的に修正されたprior knowledgeを作成できることです。これはVAR-LiNGAM単体に設定できるprior knowledgeが即時効果のパスのみであることよりも優れています。※
(※VAR-LiNGAMでは、lingam_modelという引数に、prior_knowledge引数を設定したDirectLiNGAMを設定することで即時効果に対してのみprior knowledge制約を設けることができます。)
この方法をSCPに応用することで、遅延効果に対してもLLMによってドメイン知識からの評価を行うことができます。
マーケティングデータに実装した結果
この擬似VAR-LiNGAMをSCDのアルゴリズムとして、前回同様の売上・ウェブサイトデータから統計的因果探索を行い、LLMで知識を補強して最終的な因果探索を行うStatistical Causal Prompting (SCP) フレームワークを一通り行ってみます。なお、過去項を追加することで変数が倍に増えるため、可視化のしやすさを考慮し変数を11個に絞りました。
おさらいですが流れはSCPの流れは以下の通りです。
- 統計的因果探索(SCD)を実行する
- LLMに対して「SCDで得られた因果関係」を提示し、ドメイン知識的に適切かを問う
- 生成された説明を踏まえて、再度LLMに因果関係の存在が妥当である確率を問う
- 得られた確率から、事前に設定した閾値によってエッジの存在を強制、不明、禁止に振り分け、prior knowledgeという制約(隣接行列)を作る
- 必要な場合はprior knowledge内のエッジの循環を削除する
- prior knowledgeを組み込んで再度SCDを行う
そしてここでSCDは前述の擬似VAR-LiNGAMを用います。
Step 1. 統計的因果探索(SCD)を実行する
まず最初のSCDを行った結果です。なお、現在期の変数は_t、1期前の変数は_t-1のラベルがついています。
図7:1回目のSCDの結果
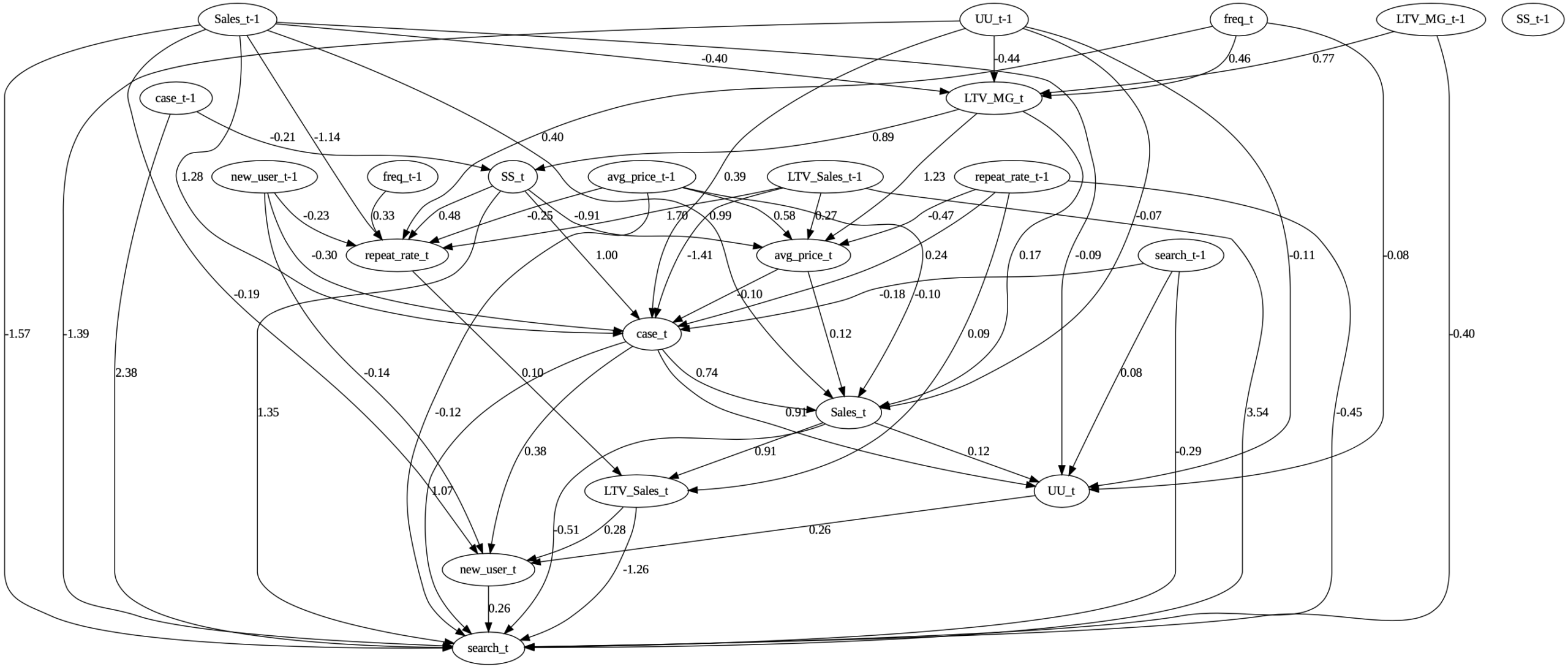
この図では、1期前の売上やユニークユーザーなどが最上流に位置しています。それがなぜか当期の利益ベース顧客生涯価値に影響し、続けて中盤は他のさまざまな変数が当期のリピート率、平均価格、申込数に影響を与え、それが売上、売上ベース顧客生涯価値、最後には新規ユーザー数、検索数へと繋がっています。
これは統計的に導かれた図であるため、直感的にはよく分からないものになってしまっています。
次にこの結果をLLMに参照してもらい、変数間のエッジが妥当かを判断してもらいます。
Step 2. LLMによる知識生成
ここでは
- LLMに対して「SCDで得られた因果関係」を提示し、ドメイン知識的に適切かを問う
- 生成された説明を踏まえて、再度LLMに因果関係の存在が妥当である確率を問う
を行って、SCDの結果がどれほど妥当であるかを確率で評価します。そして、95%以上の確率で妥当であると回答されたエッジのみを描画すると以下のようになります。
図8:LLMに生成されたprior knowledge
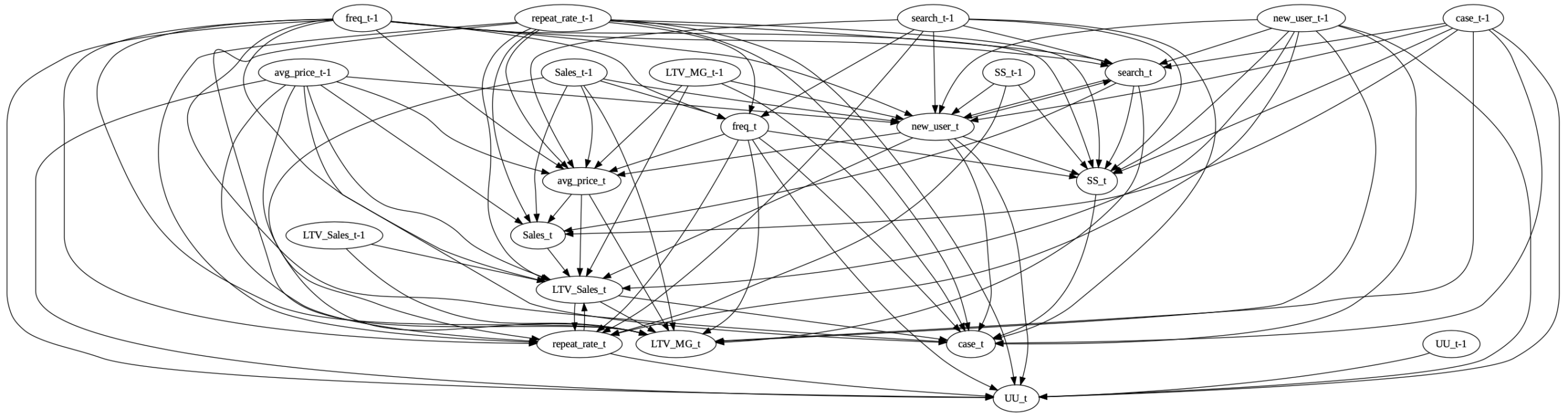
この図には、エッジの循環が二箇所ではありますが存在しています。search_tとnew_user_tの間、そしてLTV_Sales_tとrepeat_rate_tの間です。DirectLiNGAMはprior knowledgeが循環を形成していると使えないため、循環を切る必要がありますが、切り方が複数あります。次のステップではその中から統計的に最善の構造を選びます。
Step 3. prior knowledgeのDAG化
prior knowledgeを循環がなくなるようにするには、循環を形成しているエッジを消去していきます。しかし消去する順番により構造が異なります。今回では2つのエッジで形成される循環が2つなので切り方は4パターンあります。その中から最善のものを選ぶ方法として、すべてのパターンの構造において構造方程式モデリング(回帰分析)を行って、データに最も適合しているものをBIC基準で選びます。
循環を切った後の、BIC基準で得られた最も良いprior knowledgeが以下のようになります。
図9:生成されたprior knowledgeのDAG化
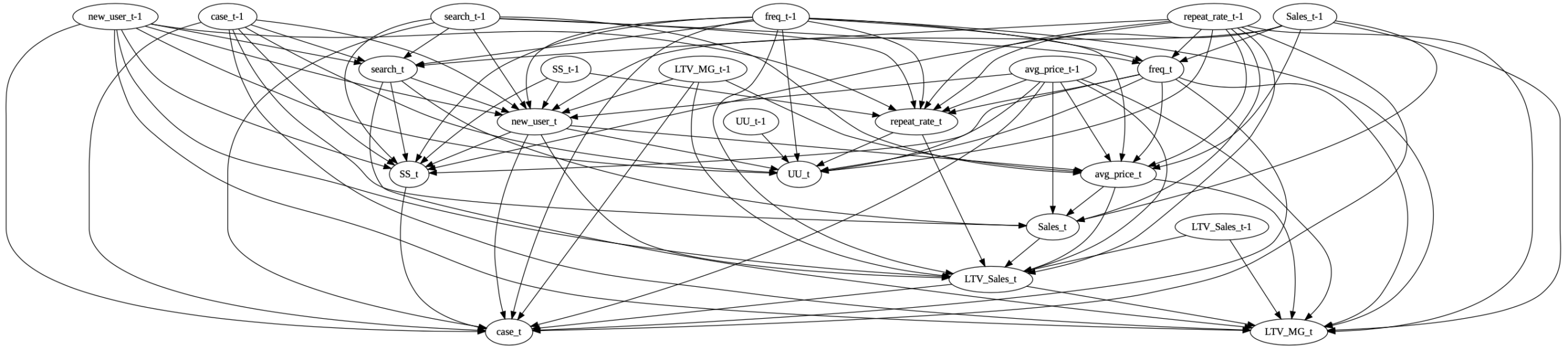
search_tとnew_user_tの循環ではsearch_tからnew_user_tへのエッジ、そしてLTV_Sales_tとrepeat_rate_tの循環ではrepeat_rate_tからLTV_Sales_tへのエッジが選択されました。統計的な比較の結果ではありますが、解釈の面でも都合の良いエッジが選択されています。
この事前知識グラフも考察しがいがありますが、今回は深入りせず、この制約を用いた因果探索を行ってその結果を考察します。
Step 4. prior knowledge制約を用いたSCD
最後に、LLMで生成しDAG化したprior knowledge制約を用いてもう一度擬似VAR-LiNGAMを行います。擬似VAR-LiNGAMにすることで、即時効果と遅延効果両方に制約を設けた状態で因果探索を行えます。
結果は以下のようになりました。
図10:prior knowledgeを用いたSCDの結果

一見するとごちゃついていますが、最下流を見るとLTV系の指標があり、その前には当期のサイトセッション、売上、ユニークユーザーなどが中盤の変数として存在しています。最上流には1期前の売上があり、1段下のその他の1期前変数と一緒に当期新規ユーザーに影響していることがわかります。
もう少し見やすくするために、描画するエッジの係数の閾値を0.05から0.3まで上げてみました。
図11:閾値を上げた簡略図
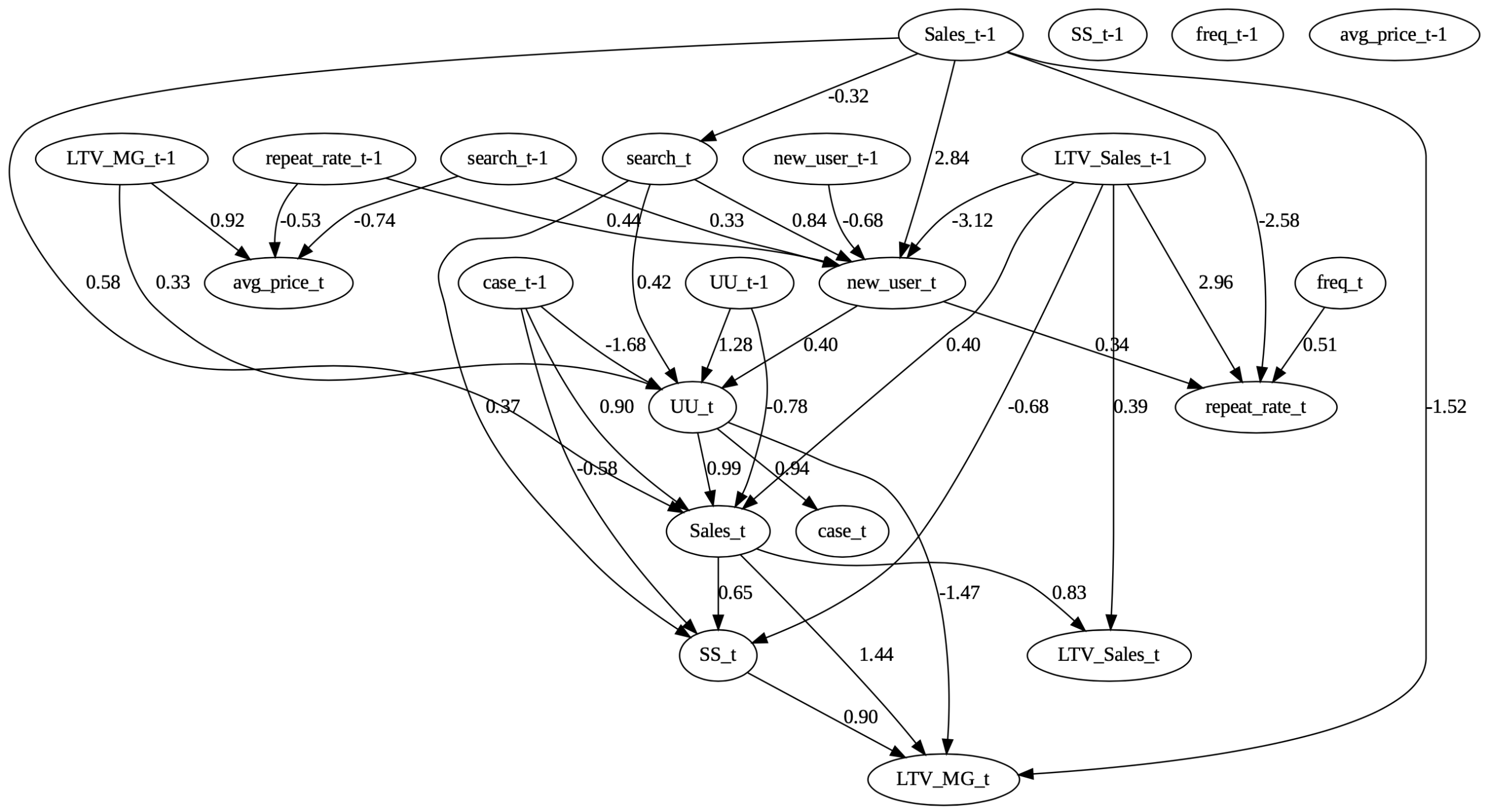
エッジの係数が小さいものが描画されなくなり、強度の強いエッジのみが現れて見やすくなりました。
最下流が1回目のSCDでは検索数(search_t)であったのに対し、今回は利益ベース顧客生涯価値(LTV_MG_t)が最下流であり、過去の売上成績から今期の検索、ユーザー数を伝って売上そして顧客生涯価値へと繋がる道が形成されており、自然な因果の流れとなっています。
ストーリーとして読み解くと、
「売上(Sales_t-1)や売上ベース顧客生涯価値(LTV_Sales_t-1)などを含む多くの変数が、次期の新規ユーザー数(new_user_t)を増加させ、ユニークユーザー数(UU_t)、リピート率(repeat_rate_t)が上昇し、売上(Sales_t)が伸びて結果的に顧客生涯価値(LTV_MG_t, LTV_Sales_t)も高まる。」
といった感じです。
LLMによってエッジが調整されたことで、統計的因果探索の結果に対し納得のいく解釈がしやすくなったことがわかります。
擬似的なVARモデルを用いて、自動でかつより直感的なパス図を導くことができました。
ただし問題点もいくつかあります。
例えばprior knowledgeに存在しなかった、当期の売上(Sales_t)とサイトセッション(SS_t)の間の関係は、売上からサイトセッションへのエッジが2回目の統計的因果探索で出現しており、これは直感的ではありません。
また、前期売上(Sales_t-1)と当期検索数(search_t)の関係がマイナスであり、売り上げが伸びているのに検索数が減るのは少し違和感があります。場合によっては売上が大きく上昇した後に需要が落ち込み気味な可能性もありますが、パスの係数の正しさは後に効果検証を行ったりした上で適切に判断する必要があります。(前述の擬似VAR-LiNGAMの実験と似た問題が発生している可能性もあります。)
このような細かな精度の問題は起こりうることは理解する必要があります。
まとめ
今回はDirectLiNGAMでVAR-LiNGAMのようなVARモデルを表現することで、SCPフレームワークを時系列因果探索に応用してみました。
LLMの存在により、データ駆動の時系列因果探索にLLMを応用することで、より自然な因果構造を作ることができました。
マーケティング施策の効果検証には、時系列モデルの仮説を迅速に作る必要があり、そのためのデータ駆動で自動的な因果探索としてSCPフレームワークが発揮できるポテンシャルは大きいと言えます。
今回用いた擬似VAR-LiNGAMの手法は特殊な前提の上に成り立っているため、どのようなデータにも汎用的に使えるものではありません。そのため、今後はまた別の方法を試していきたいと思います。
関連ブログ
Statistical Causal Prompting (SCP) 実装レポート:因果探索をLLMで強化する
参考文献
[^1]: Takayama, Masayuki; Okuda, Tadahisa; Pham, Thong; Ikenoue, Tatsuyoshi; Fukuma, Shingo; Shimizu, Shohei; Sannai, Akiyoshi (2024). Integrating Large Language Models in Causal Discovery: A Statistical Causal Approach. arXiv:2402.01454.

